t≤2, t≥3
Объяснение:
все выражение находится под корнем. Корень имеет смысл, когда подкоренное выражение больше или равно нулю:
t²-5t+6≥0
найдем корни квадратного трехчлена, для этого приравняем его к нулю:
t²-5t+6=0
по теореме Виета: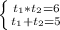 
, откуда корни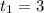 
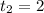
отметим точки на прямой (рис) (закрашенными, т.к наше неравенство нестрогое)
знаки начинаются с +, дальше чередуем.
у нас ≥, выбираем +
t ∈ (-∞; 2] ∪ [3; +∞), что можно понимать, как: нас устраивает t меньше 2 и 2 включительно и больше 3, включая 3 => t≤2, t≥3
Якщо x < 0, то вираз √25х² можна спростити наступним чином:
√25х² = √(25 * х²) = √25 * √х² = 5 * |x|, де |x| - модуль числа x.
Отже, спрощений вираз √25х² для x < 0 дорівнює 5 * |x|.