· Для того, чтобы построить высоту остроугольного треугольника, проведите из его вершины прямую, перпендикулярную противолежащей стороне. Отрезок, соединяющий точку пересечения перпендикулярных прямых и вершину, и будет являться вершиной треугольника, опущенной из заданной высоты. При этом все три высоты остроугольного треугольника должны лежать внутри треугольника.
· В случае тупоугольного треугольника, для того, чтобы построить высоты, опущенные из двух его острых углов, необходимо продолжить прямые, содержащие стороны, прилегающие к тупому углу. Высота, опущенная из острого угла тупоугольного треугольника, лежит на продолжении противолежащей вершине стороны, за пределами треугольника.
· Если один из углов треугольника прямой, то стороны треугольника, прилегающие к прямому углу (катеты) уже являются его высотами (совпадают с высотами треугольника). Третья высота прямоугольного треугольника, проведенная к его гипотенузе, лежит внутри пределов сторон треугольника.


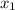 =-4,
=-4, 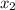 =4
=4 ,
, 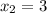
Для построения графика функции y = -x² + 2x + 3, давайте сначала построим таблицу значений, затем нарисуем график и ответим на ваши вопросы:
x | y
--+
-2 | 7
-1 | 2
0 | 3
1 | 4
2 | 3
3 | 0
Теперь давайте построим график, используя эти точки:
|
7 + *
| *
|
4 + *
| *
|
3 + *
| *
|
2 + *
|
| *
0 +
|
-2 -1 0 1 2 3
ответы на ваши вопросы:
1) Функция y = -x² + 2x + 3 принимает положительные значения в интервалах (-2, -1) и (2, 3). Она принимает отрицательные значения в интервале (-1, 2).
2) Функция убывает на интервалах (-∞, -1) и (1, ∞). Она возрастает на интервале (-1, 1).
3) Наименьшее значение функции составляет y = 0, которое достигается при x = 3. Наибольшее значение функции составляет y = 7, которое достигается при x = -2.
Помимо этого, построим график для функции y = 2x² + 2x - 4:
```
|
10 + *
| *
|
5 + *
| *
|
0 + *
| *
|
-5 + *
|
| *
-10 +
|
-2 -1 0 1 2 3
```
Из этого графика можно сделать те же выводы по вопросам 1-3, но с другими значениями.