Для определения наибольшего и наименьшего значений функции f(x) = x^3 - 3x на промежутке [-2; 0] необходимо найти критические точки на этом промежутке. Критические точки являются точками, где производная функции равна нулю или не существует.
Давайте начнём с нахождения производной функции f(x):
f'(x) = 3x^2 - 3
Чтобы найти критические точки, приравняем производную к нулю и решим уравнение:
3x^2 - 3 = 0
Решив это уравнение, получим:
x^2 - 1 = 0
(x - 1)(x + 1) = 0
Из этого следует, что критическими точками являются x = -1 и x = 1.
Теперь вычислим значения функции f(x) в этих точках и на концах промежутка:
f(-2) = (-2)^3 - 3(-2) = -8 + 6 = -2
f(0) = 0^3 - 3(0) = 0
Таким образом, наименьшее значение функции f(x) на промежутке [-2; 0] равно -2, а наибольшее значение отсутствует, так как функция не имеет максимума на данном промежутке.
Объяснение:
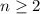 равных частей
равных частей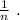
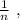 нужно разрезать верёвочку длины 2 на
нужно разрезать верёвочку длины 2 на 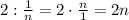 частей.
частей. частей.
частей.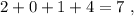 не делится на три.
не делится на три.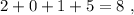 не делится на три.
не делится на три.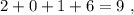 делится на три!
делится на три!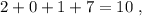 не делится на три.
не делится на три. не делится на три.
не делится на три.
Объяснение:
застосування похиднои