2x² + 7x - 4 = 0
Это квадратное уравнение решения много, самый частый -- через дискриминант (D).
Квадратное уравнение в общем виде выглядит так:
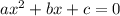
где a, b, c -- коэффициенты, a ≠ 0
Формула дискриминанта:
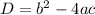
Формула корней:
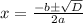
При этом от дискриминанта зависит количество корней в уравнении:
Если D > 0, то уравнение имеет 2 корня
Если D = 0, то уравнение имеет 1 корень
Если D < 0, то уравнение не имеет корней
Теперь решение:
2x² + 7x - 4 = 0
В нём a = 2, b = 7, c = -4. Подставим эти значения в формулу дискриминанта:
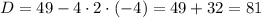
D > 0, значит уравнение имеет 2 корня.
Найдём корень из дискриминанта и корни уравнения:
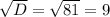
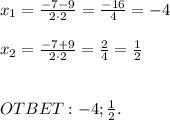
Метод интервалов: ( нужные нам промежутки со знаком (+) )
С учетом того, что:
Часть ответа:
Метод интервалов: ( нужные нам промежутки со знаком (+) )
С учетом того, что:
Часть ответа:
Объединяя ответы от 1-го и 2-го случая, получим окончательный ответ: