(4;  )
)
Объяснение:
Дотична може бути паралельна заданій прямій, якщо їх кутові коефіцієнти рівні між собою. Кажучи простими словами, спочатку нам потрібно знайти точку в якій похідна рівна 3 (y = 5 +3х ).
Знайдемо похідну від f(x) = x^3/3−4x^2+19x−7:
f'(х) = x^2 - 8x + 19
Прирівнюємо дане квадратне рівняння до похідної прямої ( y = 5 +3х; у' = 3):
x^2 -8x + 19 = 3
x^2-8x + 16 = 0
Згідно т.Вієта:
x1+x2 = 8
x1*x2 = 16
x1 = 4; х2 = 4
Але це тільки абсциса, щоб знайти ординати потрібно підставити знайдені точки в рівняння функції:
f(4) = 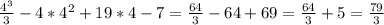
По суті, у нас два кореня рівняння x1 = 4 і x2 = 4 і ми повинні були записати дві точки, однак оскільки у нас відбулося співпадіння точок, то у відповідь можна записати одну, тобто (4;  )
)
исходи из того,что π⇔180⁰
значит х ⇔40⁰ х=40π/180=2π/9
80⁰ х=80π/180=4π/9
120⁰ х=120π/180=6π/9
160⁰ х=160π/180=8π/9
для синусов чем больше угол,тем больше синус (для 1 четверти)
sin 120⁰ =sin 60⁰
sin 160⁰=sin 20⁰
теперь пишем в ряд возрастания
8π/9 ; 2π/9 ; 6π/9 ; 4π/9
2)5π/8 это х
π⇔180⁰ х=5π/8 *180/π=122,5⁰
7π/12 х=7π/12*180/π=105⁰
11π/12 х=11π/12*180/π=165⁰
47π/9 х=
ой надо уйтти,но тут и сама дорешаешь
Определим функцию:
Всё, что от нас требуется - обеспечить единственное решение (три равных корня)
Если бы h(x) была, к примеру, параболой - можно было найти все значения b для которых справедливо равенство Δ=0 (следовательно - для которых есть единственное решение), но в данном случае у нас рациональная функция, потому нужен другой метод.
Легко проверить что
Пусть выполняется
x=3 был исключён из области определения тут:
что и требовалось. А значения b, выполняющие условие:
Реверсия. Для
ответ:
Если возникнут вопросы - дайте знать.