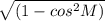
(2+√5) = 1/8 + 3√5/8 + 15/8 + 5√5/8 = (1/2 + √5/2)³ = (1 + √5)³/8
(2 - √5) = 1/8 - 3√5/8 +15/8 - 5√5/5 = (1/2 - √5/2)³ = (1 - √5)³/ 8
∛(2 + √5) + ∛(2 - √5) = ∛(1 + √5)³/2³ + ∛(1 - √5)³/2³ = (1 + √5)/2 + (1 - √5)/2 = 1/2 - √5/2 + 1/2 + √5/2 = 1
ответ ОДИН
сделаем по другому
a = 2 + √5
b = 2 - √5
∛(2 + √5) + ∛(2 -√5) = c
∛(a*b) = ∛((2 + √5)(2 - √5)) = ∛(-1) = -1 (формула 1)
a + b = 2 + √5 + 2 - √5 = 4 (формула 2)
∛a + ∛b = c
∛a = c - ∛b (возводим в куб) (формула 3)
a = c³ - 3c²∛b + 3c∛b² - b
c³ = a + 3c²∛b - 3c∛b² + b = a + b + 3c∛b(c - ∛b) ={ по формуле 2 и 3} = 4 + 3c∛b*∛a = {формула 1} =4 - 3c
c³ + 3c - 4 = 0
c³ + c² + 4c - c² - c - 4 = 0
c²(c - 1) + c(c -1) + 4(c-1) = 0
(c - 1)(c² + c + 4) = 0
вспоминаем что ∛(2 + √5) + ∛(2 -√5) = c
первая скобка c = 1
вторая скобка c² + c + 4 = 0 D=1 - 4*4 = -15 дискриминант отрицательный, действительных решений нет (2 комплексных)
ответ 1
одна сторона пусть x другая y
тогда
2x+2y=80
x+y=40 x= 40 - y
s1 = xy
s2 = (x+8)(y+2)
(x+8)(y+2)/1,5= xy
8y + 16+2x -0,5 xy = 0
8y +16 + 2 ( 40-y) - 0,5 ( 40-y)y=0
8y + 16 +80 - 2y - 20y + 0,5 y*y=0
y^2-28y +192=0
корни ( 28 (+-) 4 )/2
16 12
x = 24 28
ответ - x = 24 y = 16
x= 28 y= 12
2) x^2 +6x = p
p^2 +5p -24 = 0
(-5 (+-)11)/2
3 -8
x^2 +6x -3 = 0
-3 (+-) ( корень из 12)
x^2 +6x +8=0
-3 (+-)(корень из 3)
4) 2a1+6d = 42 <=> 2a1= 42 - 6*3 = 24 <=> a1 = 12
a3+7d-a3=21 <=> d=3
3) - 0,1
cos M = MK / MP, отсюда MK = cosM * MP = √7/4 * 8 = 2√7
по теореме Пифагора: PK = √(MP² - MK²) = √(64-28) = √36 = 6
ответ: 6