По формуле:
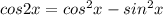
Зная это получаем:
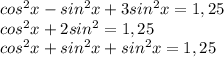
Известно что:
отсюда получаем:
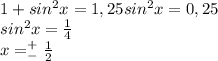
Получаем 2 уравнения:
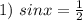это табличное значение синуса и получается 2 решения:
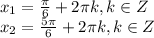
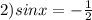аналогично получаем 2 решения:
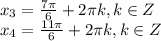
Теперь обратим внимание, что эти 4 решения можно записать в 2 решения в виде:
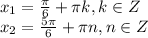
Теперь надо найти при каких значениях k и n решения лежат на отрезке ![[0; \frac{5\pi}{2}]](/tpl/images/0071/0603/9e0ce.png)
Для этого решаем 2 неравенства
1) 
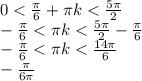
Так как к у нас принадлежит целым числам, то получается что к=0,1,2
2) Теперь ищем n, аналогично:
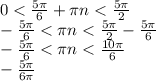
Поскольку n принадлежит целым числам, то получается что n=0,1
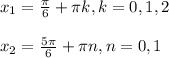
давайте покажу два примера:
для решения задания нам для начала нужно знать теорему Виета
она выглядит вот так:
если наше квадратное уравнение выглядит так x² + px + q = 0, то
x1 + x2 = -p
x1 · x2 = q
судя по первому примеру -1+3=2
-1*3=-3
тогда наше уравнение будет выглядеть так х^2+2x-3=0
следущий пример точно также: -0,2+(-0,3)=-0,5
-0,2*(-0,3)=0,06
а уравнение-x^2-0.5x+0.06=0
Желаю удачи!
потом подставляем вместо Х верхний предел, отнимаем нижний
и оля готово!