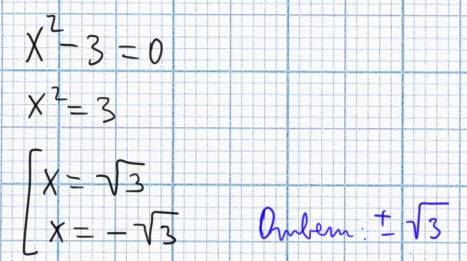
Решите уравнение методом разложения на множители
1) √x⁵-3√x³-18√x= 0 ОДЗ : x≥0
x²√x -3x√x -18√x =0⇔ √x(x² -3x -18) =0 ⇔x(x -6)(x+3) =0
x =0 ; x =6 ; x = - 3 ∉ ОДЗ →посторонний корень.
2) ⁴√х⁹-2⁴√х⁵-15⁴√х=0 ОДЗ : x≥0
x²(⁴√х -2x⁴√х-15⁴√х) =0 ⇔ - 16⁴√х *x² =0 ⇒ x =0
Решите уравнение методом введения новой переменной
3) √(x²+1 - 2x )- 6√(x-1) = 7
√(x - 1 )² - 6√(x-1) = 7 ; замена : t =√(x-1) ≥ 0
t² -6t -7 = 0 ⇒ по Виету t₁ = 7 ; t₂= - 1 →посторонний
или t₁/₂ = 3 ± 4 * * * √D₁ = √(3² -(-7) ) =√(9+7) =√16 =4; D₁ =D/4 * * *
√(x-1) =7 ⇔x- 1 =7² ⇒ x= 50 .
* * *ИЛИ t² -6t -7 =0 t² -7t +t -7 =0 ⇔t(t -7) +(t -7) =0⇔(t -7)(t+ 1) =0 * * *
4) √(x²-4x+4) - 6=5√(2 -x)
√(2-x)² - 6 = 5√(2 -x) замена : t =√(2-x) ≥ 0
t² -5t -6 =0 ⇒ по Виету t₁ = 6 ; t₂= - 1 →посторонний
√(2 -x) =6 ⇔2 - x =6²⇒ x = 2 -36 = -34 .
Решите уравнение, используя функционально-графические методы
5) 2ˣ = 6-x
у₁ =2ˣ → (возрастающая показательная функция: 2 >1 ) ;
{ ...(- 2 ; 1/4) , (- 1 ; 1/2) , (0 ; 1) , (1; 2) , (2 ; 4) ; ...} ∈ графику
y₂ = - x +6 → ( ||y = kx+b || убывающая линейная функция: k = - 1 < 0 ).
{ (0 ;6) , (6 ; 0) . || (2 ; 4) } ∈ графику y₂
* * * графики постройте самостоятельно * * *
Пересечением графиков функций у₁ и y₂ получается ответ
x = 2 .
6) (1/3)ˣ= x + 4
у₁ = (1/3)ˣ → (убывающая показательная функция: 0<1/3<1)
{ ... (- 2 ; 9 ) , (-1; 3) , (0 ; 1) ; (1; 1/3) , (2 ; 1/9) ; ...} ∈ графику
у₂ = x + 4→ ( возрастающая линейная функция : k = 1 > 0)
{ ( - 4 ; 0) ; (0; 4) . || (-1 ; 3) }
x = -1 .
1). 1,6x - 2,5 = 4,1x 2). -2x - 20 = 7x + 43
4,1x - 1,6x = -2,5 7x + 2x = -20 - 43
2,5x = -2,5 9x = -63
x = -1 x = -7
3). -16 -1,5x = 43,8 + 3,1x 5). 7·(7 + y) - 4y = 4y - 67
3,1x + 1,5x = -16 - 43,8 7y - 4y - 4y = -67 - 49
4,6x = -59,8 -y = -116
x = -13 y = 116
4). 0,9 + 7 + (-6,53k) = 12 + 0,9 - 6,73k
6,73k - 6,53k = 12,9 - 7,9
0,2k = 5
k = 25
x^2/3=3
x^2=9
!x!=3
x=3
x=-3