ответ: x1=2 ;x2=4
Объяснение:
(x-2)^6+(x-4)^6=64
Вычтем и прибавим удвоенное произведение:
(x-2)^6 -2*(x-2)^3*(x-4)^3 +(x-4)^6 +2*(x-2)^3*(x-4)^3=6
( (x-2)^3-(x-4)^3 )^2 +2*(x-2)^3*(x-4)^3=64
( ( (x-2)-(x-4) )*( (x-2)^2 +(x-4)^2 +(x-2)*(x-4) ) )^2 +2*(x-2)^3*(x-4)^3=64 ( формула разность кубов)
т.к (x-2)^2+(x-4)^2= ( (x-2)-(x-4))^2+2*(x-2)*(x-4)= 4+2*(x-2)*(x-4)
4* ( 4+3*(x-2)*(x-4) )^2 +2* ( (x-4)*(x-3) )^3=64
Замена : (x-2)*(x-4)=t ( x^2-6x+8=t → (x-3)^2-1=t → t+1>=0→ t>=-1)
4* (4+3t)^2 +2*t^3=64
2* (4+3t)^2+t^3=32
2*(16+24t+9t^2) +t^3=32
32+48*t+18*t^2+t^3-32=0
t^3+18*t^2+48*t=0
t*(t^2+18t+48)=0
t1=0
t^2+18t+48=0
D/4=81-48=33
t2=-9+√33 < -9+√36=-3<-1 (не подходит)
t3= -9-√33 <-1 (не подходит)
Таким образом единственное решение t=0.
Вернемся к замене:
(x-2)*(x-4)=0
x1=2
x2=4
ответ: x1=2 ;x2=4
Если P(x) делится на Q(x), то
P(x)/Q(x)=A(x) ,где A(x)-многочлен.
Поскольку Q(x) делится на P(x),то
Q(x)/P(x)=B(x) ,где B(x) -многочлен.
Откуда верно, что:
A(x)*B(x)=1
Если знаете комплексный анализ, то очевидно, что многочлен со степенью больше нуля имеет хотя бы один корень (комплексный или действительный),но тогда и произведение многочленов должно иметь этот корень,но многочлен C(x)=A(x)*B(x)=1 ,не может иметь корней тк 1 не равно 0.
А значит оба многочлена A(x) и B(x) имеют нулевую степень (константы),таким образом B(x)=c.(с не равно 0)
Q(x)=c*P(x)
Пусть многочлен A(x) имеет степень n ,а многочлен B(x) имеет степень m.Тогда очевидно, что многочлен A(x)*B(x) имеет степень m+n, но 1 это многочлен нулевой степени:
m+n=0
Тк m>=0 и n>=0, то m=n=0.
То есть B(x)=c (с не равно 0)
Q(x)=c*P(x) ,что и требовалось доказать.
вторая скобка положительна в силу неотрицательности p, поэтому остается только p=1;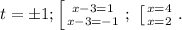
ответ: 4; 2