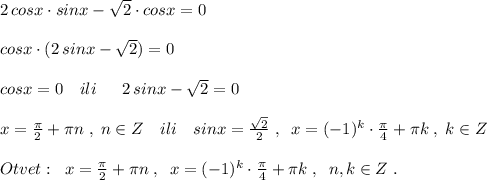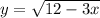
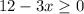
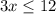
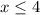
![(-\infty; 4]](/tpl/images/0070/2199/7ba5a.png)
√12-3x
12-3x≥0
-3x≥-12 /(-3)
x≤4
x∈(-бесконечности;4]
Речь идёт о площадях подобных треугольников.
Их площади относятся как квадраты коэффициентов подобия.
Размеры светлого треугольника: основание равно 1-(-1) = 2, высота равна 2-0 = 2. Его площадь S1 = (1/2)2*2 = 2 кв.ед.
Треугольник, состоящий из светлого и закрашенной фигуры, имеет высоту, равную 2-(-1) = 3.
То, что они подобны видно по рисунку - основания треугольников параллельны. То есть они попадают под следствие: прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник.
Коэффициент подобия определяем по соотношению высот и он равен 3/2.
Площадь большего треугольника S2 = S1*(3/2)² = 2*(9/4) = 9/2 кв.ед.
ответ: S3 = S2 - S1 = (9/2) - 2 = 5/2 кв.ед.
Если уравнение делить на cosx, то надо оговориться, что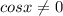 
, так как на 0 делить нельзя. В силу этого можно потерять корни уравнения, при которых cosx обращается в 0, это 
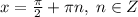. Тогда надо отдельно проверить, не являются ли 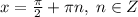корнями заданного уравнения, подставив их в это уравнение.
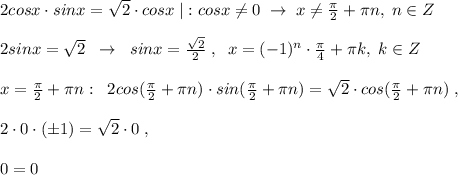
Так как получили верное равенство, то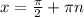 
являются корнями заданного уравнения.
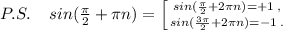
Чтобы не проводить лишнюю проверку , при решении уравнения надо просто вынести общий множитель cosx за скобку, тогда сразу получим две серии решений:
