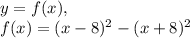
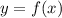— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 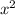(не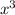 
, не 
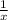, не 
и не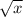 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид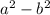 
, где 
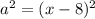, и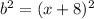 
. Формула «разность квадратов» раскрывается так: 
.
.
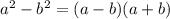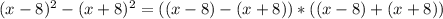
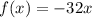, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
4.5z^2-9z+4=0; D=81-72=9; z1=(9-3)/(2*4.5)=2/3; z2=(9+3)/(2*4.5)=4/3. m^2=2/3; m1=корень(2/3); m2= корень(4/3).
2)Аналогично... 2,5z^2-5z-20=0; z^2-2z-8=0; D=4+32=36; z1=(2-6)/2= -3; z2=(2+6)/2=4;
n^2= -3 (не имеет смысла); n^2=4; n=2.
3) 9(81-90x+25x^2)+153-85x+8=0; 225x^2-895x+890=0; D=895^2-4*225*890=25; x1=900/450=2; x2=890/450=89/45.
4) 36x^2+12x+1+12x+2-24=0; 12x^2+8x-7=0; D=64+4*12*7=400; x1=0.5; x2= -7/6.
5) 8*(100-60x+9x^2) - 50+15x-3=0; 800-480x+72x^2-50+15x-3=0; 24x^2-155x+249=0;
D=155^2-4*24*249=121; x1=(155-11)/(2*24)=3; x2=(155+11)/(2*24)=83/24