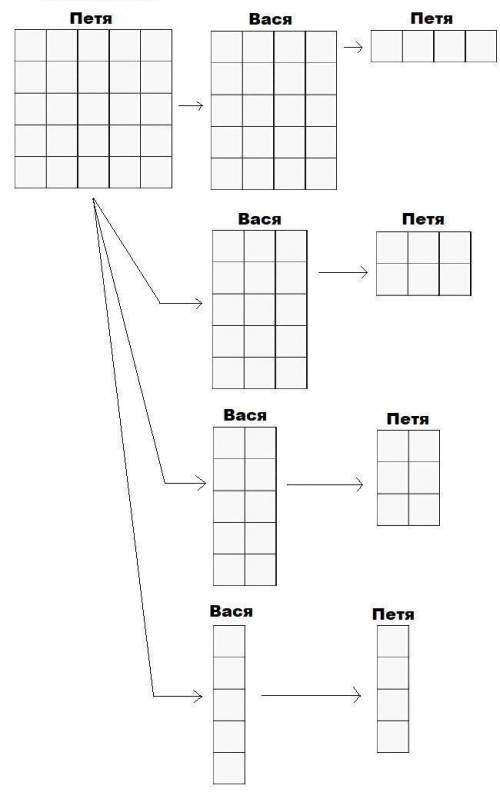
Заметим, что периметр шоколадки станет равным 10, если она будет состоять из прямоугольников 1 x 4 или 2 x 3, т. е. по одной стороне одна клетка, по другой 4 или по одной 2 клетки, по другой 3. По условию Петя начинает игру первый. Покажем, что у него существует выигрышная стратегия. Допустим, что после его очередного хода шоколадка приняла форму квадрата со сторонами 5 x 5. В этом случае, какой бы ход ни сделал Вася, Петя побеждает следующим ходом. Это наглядно показано на рисунке. Следовательно, Петина стратегия заключается в урезании шоколадки на каждом своем ходу до квадрата. На первом ходу он отламывает от шоколадки кусок 1 x 2019, превращая шоколадку в квадрат 2019 x 2019. Затем каждый раз, когда Вася отламывает n клеток по горизонтали, Петя отламывает n клеток по вертикали, превращая шоколадку в квадрат размером (2019-n) x (2019-n). В результате найдется Васин ход, после которого по горизонтали или по вертикали шоколадки останется не более пяти клеток. Следующим своим ходом Петя либо сразу побеждает, если клеток менее пяти, либо урезает шоколадку до квадрата размером 5 x 5, если клеток ровно 5. Далее после любого Васиного хода Петя побеждает согласно рисунку ниже.
Объяснение:
1.
Объяснение:
x²•|x-3|+x²-6x+9 ≤ 0
x²•|x-3|+(x-3)² ≤ 0
x²•|x-3|+lx-3l² ≤ 0
По определению модуля и квадрата
x²•|x-3| ≥ 0 и lx-3l²≥ 0, тогда и вся сумма в левой части неравенства
x²•|x-3|+lx-3l² ≥ 0.
Получили, что неравенство будет иметь решение лишь в том случае, когда
x²•|x-3|+lx-3l² = 0
lx-3l•(x^2 +lx-3l) = 0
lx-3l=0 или x^2+lx-3l=0
1) Первый множитель равен нулю при х=3.
2) Второй множитель мог бы быть равным нулю только в том случае, когда оба неотрицательных слагаемых одновременно были бы нулями при некотором значении х, но х^2= 0 при х=0, а lx-3l = 0 при х =3.
Уравнение корней не имеет.
Неравенство имеет одно целое решение: х = 3.
b2=16
b3=24
b10=80
Вот так