ответ: (1;-1).
Объяснение: Выразим из второго уравнения переменную у через переменную х.
у=2-3х
Подставим выражение 2-3х в первое уравнение вместо переменной у.
2х-3(2-3х)=5
2х-6+9х=5
2х+9х=5+6
11х=11
х=11:11
х=1
Подставим значение х в выражение у=2-3х.
у=2-3*1
у=2-3
у=-1.
Сделаем проверку: 2*1-3*(-1)=5 3*1+(-1)=2
2+3=5 3-1=2
5=5 2=2
Итак, у нас есть ряд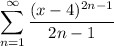 
.
Вычислим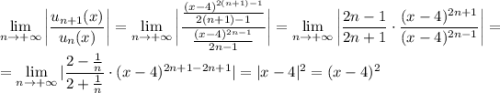 
Вот это уже хорошо. Нужно, чтобы это выражение было меньше единицы (это из признака Даламбера), тогда мы найдем те самые х, при которых ряд будет сходиться.
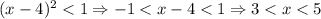
Вот мы их получили. Но теперь нужно проверить концы: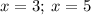 
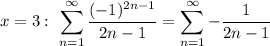
Что можно сказать об этом ряде? Допустим, мы будем использовать предельный признак сравнения. Есть известный ряд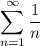 
, он расходится, при этом предел отношения n-ых членов полученного ряда и приведенного не равен 0, а равен конкретной константе (-1/2, если делить n-ый член полученного на n-ый член ряда 1/n), так что при 
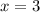ряд расходится.
Аналогичная история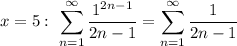 
Все те же рассуждения, только предел отношения будет равен 1/2. То есть при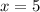 
ряд расходится.
ответ: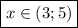 
а)47*15+53*15 = 15 * (47 + 53) = 15 * 100 = 1500
б)29*72-29*22 = 29 * (72 - 22) = 29 * 50 = 1450
в)9,3*34+16*9,3 = 9,3 * (34 + 16) = 9,3 * 50 = 465
г)8,3*18-18*5,8 = 18 * (8,3 - 5,8) = 18 * 2,5 = 45