Даны последовательные члены геометрической прогрессии
b₁ = 3x - 2; b₂ = x+2; b₃ = x+8
По свойству членов геометрической прогрессии
b₂² = b₁*b₃
(x + 2)² = (3x - 2)(x + 8)
x² + 4x + 4 = 3x² + 24x - 2x - 16
x² - 3x² + 4x - 22x + 4 + 16 = 0
-2x² - 18x + 20 = 0 | : (-2)
x² + 9x - 10 = 0
Корни по теореме, обратной т. Виета
(x + 10)(x - 1) = 0
x₁ = -10; x₂ = 1
1) b₁ = 3x-2 = 3*(-10)-2 = -32;
b₂ = x+2 = -10 + 2 = -8;
b₃ = x+8 = -10 + 8 = -2
Проверка:
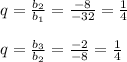
-32; -8; -2; - геометрическая прогрессия со знаменателем q=1/4
2) b₁ = 3x-2 = 3*1-2 = 1;
b₂ = x+2 = 1 + 2 = 3;
b₃ = x+8 = 1 + 8 = 9
Проверка:
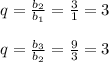
1; 3; 9; - геометрическая прогрессия со знаменателем q=3
ответ: при x₁ = -10; x₂ = 1
211евляется квадратным натуральным числом