ответ: 1) x = (a + b) / (a - b); a ≠ b; 2) x = 2 · (m - n); 3) x = a + 1;
4) x = (3 · (m - n)) / (m + n); m ≠ - n
Объяснение:
1) a²x - b²x = a² + 2ab + b²; x · (a - b) · (a + b) = (a + b)²; x = (a + b)² / (a - b) · (a + b)
x = (a + b) / (a - b); a ≠ b
2) 3mx + 3nx = 6m² - 6n²; 3 · x · (m + n) = 6 · (m + n) · (m - n);
x = (6 · (m + n) · (m - n)) / 3 · (m + n); x = 2 · (m - n)
3) ax + x = a² + 2a + 1; x · (a + 1) = (a + 1)²; x = (a + 1)² / (a + 1) = a + 1; x = a + 1
4) m²x + 2mnx + n²x = 3m² - 3n²; x · (m + n)² = 3 · (m + n) · (m - n);
x = (3 · (m + n) · (m - n)) / (m + n)²; x = (3 · (m - n)) / (m + n); m ≠ - n
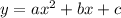
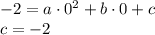
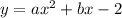
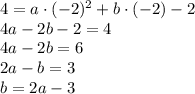
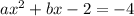имело ровно один корень, то есть равный нулю дискриминант: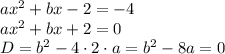
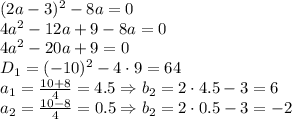
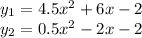
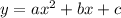
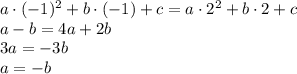
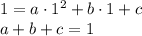
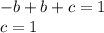
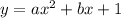
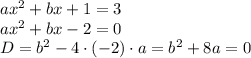
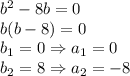
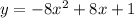
Очевидно, что каждая сторона многоугольника связывает две соседние вершины, так ведь? Это означает, что если мы возьмём k-ую вершину, то у неё есть два ближайших соседа - это (k+1)-ая вершина и (k-1)-ая. и с этими соседями k-ая вершина связана двумя сторонами многоугольника. Пока понятно, надеюсь?
ну а дальше просто. единственный выпуклый многоугольник, который не имеет диагоналей, - это треугольник, так ведь? у треугольника все вершины связаны сторонами треугольника, и никакими другими прямыми линиями мы не можем связать вершины.
следовательно, для подсчёта количества диагоналей в выпуклом N-угольнике надо вычесть количество треугольников (каждый из которых построен по соседним k, k+1 и k-1 вершинам) из общего количества прямых линий, которые мы можем провести от k-ой вершины до всех остальных N-1 вершин.
Количество треугольников посчитать несложно - оно равно количеству вершин, т. е. N штук треугольников. Теперь посчитаем количество прямых линий от k-ой вершины до остальных N-1 вершин. Очевидно, что оно равно N-1 прямых линий (с учётом сторон N-угольника) .тогда для N вершин имеем
N * ( N - 1 ) (1)
штук прямых линий. теперь учтём, что каждую такую линию мы посчитали дважды (когда проводили её от k-ой вершины к m-ой и снова от m-ой вершины к k-ой) и поделим выражение (1) пополам:
N * ( N - 1 ) / 2.
ну вот, а теперь из этого вычтем кол-во треугольников, получим кол-во диагоналей Ld:
Ld = N * ( N - 1 ) / 2 - N = ( N * N - N - 2 * N ) / 2 = N * ( N - 3 ) / 2.
для вашего случая, когда Ld = 77, получаем квадратное уравнение:
N * N - 3 * N - 154 = 0
N = ( 3 + sqrt ( 9 + 4 * 154 ) ) / 2 = 14.