Объяснение:
а) 9x-3y=6;
Выражаем у через х и получаем линейную функцию:
3у=9х-6;
у=(9х-6)/3=3х-2;
у=3х-2.
Графиком линейной функции является прямая, прямую можно построить по двум точкам, например:
х у
0 -2
2 4
См. рисунок а).
б) y=-4x+2;
График линейной функции - прямая, строим ее по двум точкам, например:
х у
0 2
1 -2
См. рисунок б).
в) y=⅓x;
График прямой пропорциональности - это прямая, которая проходит через начало координат точку О(0;0).
Строим по двум точкам, например:
х у
0 0
3 1
См. рисунок в).
г) y=-x;
График прямой пропорциональности - прямая, которая проходит через начало координат точку О(0;0).
Строим по двум точкам, например:
х у
0 0
2 -2
См. рисунок г).
д) y=-5;
Графиком является прямая, которая проходит через точку (0;-5) и параллельно оси абсцисс (ОХ).
См. рисунок д).
e) x=4;
Графиком является прямая, которая проходит через точку (4;0) и параллельно оси ординат (ОY).
Подробнее - на -
Тут разобрано два варианта, когда требуется найти вероятность, что "хотя бы три детали из пяти дефектные" и когда "ровно три детали из пяти дефектные".
Всего у нас изделий 
, изделий имеющих скрытый дефект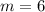 
.
Выбрать 5 изделий из 18 мы можем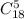 
Выбрать три дефектных, мы можем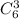 
, остальные 2 можем выбрать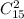 
Вероятность события, равна отношению всех исходов к числу благоприятствующих исходов.
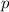(хотя бы 3 из 5 - дефектные детали)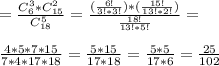 
Если в задаче требуется найти вероятность, когда у нас ровно три дефектных изделия, то меняется только количество какими мы можем вытащить оставшиеся две детали, так как нам теперь не нужно учитывать дефектные. Теперь это будет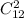 
Соответственно:
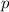(3 из 5 - дефектные детали)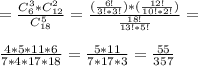 
2)60-18=42(км)
и не совсем 40 получится