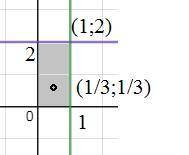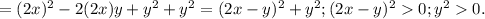
Объяснение:
Уравнение касательной имеет вид:
y=f(x_0)+f'(x_0)(x-x_0)y=f(x
0
)+f
′
(x
0
)(x−x
0
)
Дана функция:
f(x)=-x^2-4x+2f(x)=−x
2
−4x+2
Найдём значение функции в точке x₀:
f(x_0)=f(-1)=-(-1)^2-4 \cdot (-1)+2=-1+4+2=5f(x
0
)=f(−1)=−(−1)
2
−4⋅(−1)+2=−1+4+2=5
Найдём производную функции:
f'(x)=-2x^{2-1}-4=-2x-4f
′
(x)=−2x
2−1
−4=−2x−4
Найдём производную функции в точке x₀:
f'(x_0)=f'(-1)=-2 \cdot (-1) -4 =2-4=-2f
′
(x
0
)=f
′
(−1)=−2⋅(−1)−4=2−4=−2
Подставим найденные значения, чтобы найти уравнение касательной:
y=f(x_0)+f'(x_0)(x-x_0)y=f(x
0
)+f
′
(x
0
)(x−x
0
)
y=5+(-2)(x-(-1))y=5+(−2)(x−(−1))
y=5-2(x+1)y=5−2(x+1)
y=5-2x-2y=5−2x−2
\boxed{y=-2x+3}
y=−2x+3
ответ: y=-2x+3 - искомое уравнение.
Находим частные производные:
∂z/∂x=6y-18x+4
∂z/∂y=6x-18y+4
Находим стационарные точки:
{∂z/∂x=0 ⇒ 6y-18x+4=0
{∂z/∂y=0 ⇒ 6x-18y+4 =0
Решаем систему:
{ 6y-18x+4=0 ( умножаем на 3)
{6x-18y+4 =0
{ 18y-54x+12=0
{6x-18y+4 =0
cкладываем
-48х+16=0
х=1/3
y=1/3
Стационарная точка (1/3;1/3) принадлежит области ( см. рис)
Находим вторые частные производные
∂²z/∂x²=-18
∂²z/∂y²=-18
∂²z/∂x∂y=6
A=-18; B=-18: C =6
Δ=AB-C²=(-18)·(-18) -6²>0
A < 0
(1/3;1/3) - точка максимума
z(1/3;1/3)=6·(1/3)·(1/3)-9·(1/3)²-9·(1/3)²+4·(1/3)+4·(1/3)=(2/3)-1-1+(8/3)=4/3 - наибольшее значение функции
На границе
При x=0
z=-9y²+4y
Квадратичная функция при 0 ≤y ≤2
z`=-18y+4
z`=0
y=4/18=2/9 - точка максимума
z(2/9)=-9·(2/9)²+4·(2/9)=(-4/9)+(8/9)=4/9 < 4/3
z(0)=0
z(2)=-9·2²+4·2=-28
При y=0
z=-9x²+4x
Квадратичная функция при 0 ≤x ≤1
z`=-18y+4
z`=0
y=4/18=2/9 - точка максимума
z(2/9)=-9·(2/9)²+4·(2/9)=(-4/9)+(8/9)=4/9 < 4/3
z(0)=0
z(1)=-9·1²+4·1=-5 > -28
При х=1
z=6y-9-9y²+4+4y, исследуем на [0;2], 0 ≤y≤2
z(y)=-9y²+10y-5 - квадратичная функция
z`=-18y+10
z`=0
-18y+10=0
y=10/18=5/9 - точка максимума
при y=5/9
z=-9·(5/9)²+10·(5/9)-5 =- (25/9)+(50/9) -5 =-20/9
Находим значения на концах
z(0)=-5
z(2)=-9·2²+10·2-5=-21 > -28
При y=2
z=12x-9x²-9·2²+4x+4·2, исследуем на [0;1], 0 ≤x≤1
z(y)=-9x²+16x-28 - квадратичная функция
z`=-18x+16
z`=0
-18x+16=0
x=16/18=8/9 - точка максимума
при x=8/9
z=-9·(8/9)²+16·(8/9)-28 =- (64/9)+(128/9) -28 >-28
Находим значения на концах
z(0)=-28
z(1)=-9·1²+16·1-28=-21 > -28
z(1/3;1/3)=4/3 - наибольшее значение функции в области
z(1;2) =-28 - наибольшее значение функции в области