1) выражение (2−c)2−c(c+4) и найдите его значение при c=−18.в ответ запишите полученное число. 2) выражение x+9/x−3 − 6/x2−9: 6/(x+3)^2−3x − 3/x−3. 3) выражение (2−c)2−c(c+4) и найдите его значение при c=−1/8.в ответ запишите полученное число. 4) выражение 2c+4/c−2 − 4/(c−2)2: 4/c2−4−3c−2/c−2. 5) выражение (2+c)2−c(c−4) и найдите его значение при c=−1/8.в ответ запишите полученное число.
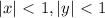
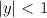 возвести в квадрат, получив,
возвести в квадрат, получив, 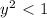 , что и требовалось проверить.
, что и требовалось проверить.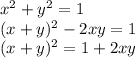
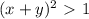
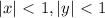 , следует, что 0 <x < 1, 0 < y < 1
, следует, что 0 <x < 1, 0 < y < 1
А остальное я незнаю
Подумай