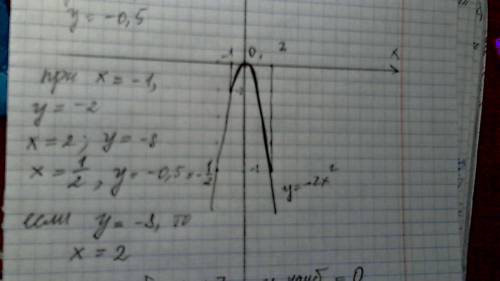
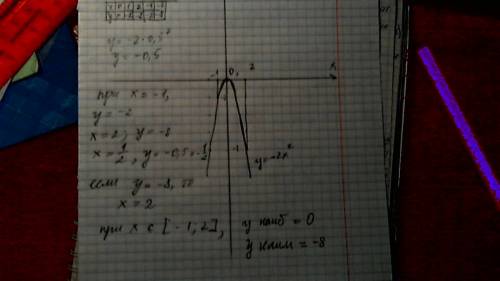
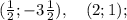
Объяснение:
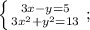
Выражаем из верхнего уравнения переменную "у":
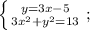
Подставляем полученное выражение в нижнее уравнение вместо "у":
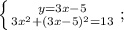
Раскрываем квадрат разности двух выражений, пользуясь следующей формулой:
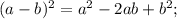
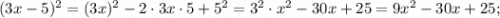
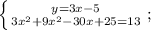
Приведём подобные слагаемые. Для этого вынесем общий множитель за скобки:
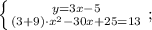
Выполним сложение в скобке и перенесём слагаемое 13 со знаком минус в левую часть уравнения:
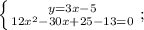
Выполним вычитание:

Разделив все части нижнего уравнения на 6, получим:

Теперь разделим все части нижнего уравнения на 2 для того, чтобы получить приведённое квадратное уравнение:
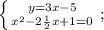
Решаем нижнее уравнение по теореме Виета. Согласно ей, сумма корней приведённого квадратного уравнения равна коэффициенту при "х", взятому с противоположным знаком, а их произведение — свободному члену:
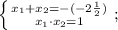
Минус перед скобкой и минус после скобки дают плюс:
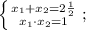
Корнями этой системы являются числа 1/2 и 2.
Мы нашли два значения переменной "х". Теперь подставим каждое из них в верхнее уравнение:
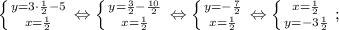
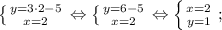
Мы получили две пары корней:
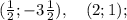
Они являются решениями системы.
1)(3x^2-12)/(1-11x)>0
3(x^2-4)/(11(1/11-x))>0
3(x-2)(x+2)/(11(1/11-x))>0
+ - + -
(-2)(1/11)(2)
(-бескон.;-2)объединено(1/11;2)
2)243*(1/81)^{3x-2}=27^{x+3}
3^{5} *(3^(-4})^{3x-2}=(3^3)^{x+3}
3^{5} *3^{-12x+8}=3^{3x+9}
3^{5-12x+8}=3^{3x+9}
3^{13-12x}=3^{3x+9}
13-12x=3x+9
-12x-3x=9-13
-15x=-4
x=4/15
3)я не уверен, что ты правильно написал функцию проверь.
Мне кажется, что f(x)=1+8x-x^2, а не как у тебя 1+8-x^2
Решу для f(x)=1+8x-x^2
f`(x)=8-2x=2(4-x)
f`(x)=0 при 2(4-x)=0
4-x=0
х=4 принадлежит [2;5)
f(2)=1+8*2-2^2=1+16-4=13
f(4)=1+8*4-4^2=1+32-16=17-наибольшее значение
f(5)=1+8*5-5^2=1+40-25=16
4)2cos(x/2)+sqrt{2}=0
cos(x/2)=-sqrt{2}/2
x/2=pi- pi/4+2pi*n
x/2=3pi/4 +2pi*n |*2
x=6pi/4+4pi*n
x=3pi/2+4pi*n, n принадлежит Z
5)16^{x} -5*4^{x}=-4
(4^{x})^{2} -5*4^{x}+4=0 |t=4^{x}
t^2-5t+4=0
t1=1; t2=4
4^{x}=1 4^{x}=4^{1}
4^{x}=4^{0} x=1
x=0
ответ: 0;1
6) log_{\frac{1}{4}}\frac{3x+2}{2x-7}=-1
(3x+2)/(2x-7)=4
3x+2=4(2x-7)
3x+2=8x-28
3x-8x=-2-28
-5x=-30
x=6
Находим ОДЗ: (3х+2)/(2х-7)>0
3(x+2/3)/(2(x-3,5))>0
+ - +
(-2/3)(3,5)
(-бескон., -2/3) объединено(3,5;+бесконечность)
х=6 входит в область определения
ответ: 6
7)27^{x}<9^{x^2-1}
3^{3x}<3^{2x^2-2}
3x<2x^2 -2
2x^2 -3x-2>0
D=25
x1=2, x2=-1/2
8){x-y=7
{log-2(2x+y)=3
{x-y=7
{2x+y=8
y=8-2x
x-(8-2x)=7
x-8+2x=7
3x=15
x=5
y=8-2*5=-2
ответ:(5;2)