Объяснение:
4 < b < 7 (1)
подобные примеры решаются просто - домножаем все части неравенства, прибавляем/отнимаем от всех частей нужные числа, пока не получим посередине, то, что требуется в доказательстве
1) надо в средней части получить 13- 3b
умножим все части (1) на -3 (здесь помним, при умножении на отрицательное число знаки неравенства меняются на противоположные)
-12 > -3b > -21 (2)
добавим ко всем частям (2) +13
-12 + 13 > 13-3b > -21 +13 или -8 < 13-3b < 1 -что и требовалось доказать
2) здесь пойдем от обратного
если 1/m < 1/n, то это значит, что m < n
и тогда из нашего ответа
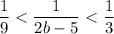
перепишем неравенство для знаменателей
получим
3 < 2b-5 < 9
теперь нам надо получить в середине b
прибавляем ко всем частям +5 и потом делим все части на 2
3+5 < 2b < 9+5
8 < 2b < 14
4 < b < 7 это и есть наша формула (1)
неравенство доказано.
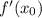производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.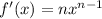
- где n это степень.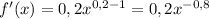
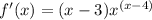
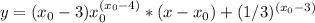
и получаешь уравнение касательной.
Представим, что у нас всего три солдата: А, В, С, тогда вариантов расстановки будет 6:
АВС, АСВ, ВАС, ВСА, САВ, СВА, то есть нам надо было просто взять факториал кол-ва солдат, а в данном случае - факториал 3 - 3!=3*2*1=6
В случае с 200 солдатами это будет факториал 200, то есть:
200!=788657867364790503552363213932185062295135977687173263294742533244359449963403342920304284011984623904177212138919638830257642790242637105061926624952829931113462857270763317237396988943922445621451664240254033291864131227428294853277524242407573903240321257405579568660226031904170324062351700858796178922222789623703897374720000000000000000000000000000000000000000000000000
Да-да, именно столько вариантов)