2 1/4=9/4
Раскроем скобки.
(1/2)х-(1/3)*(9х/4)-(1/3)*51=2х-(1/2)х+1;
(1/2)х-(3х/4)-17=2х-(1/2)х+1;
соберем члены, содержащие переменную слева, а числа справа. помня, что при переходе через знак равенства в противоположную сторону, знаки изменяются на противоположные.
(1/2)х+(1/2)х-(3/4)х-2х=17+1;
(-1 3/4)х=18
-1 3/4=-7/4
(-7/4)х=18
х=18/(-7/4)
х=-72/7
х=-10 2/7
Проверка. Подставим х= 72/7 в левую часть исходного уравнения. получим (1/2)*(-72//7)-(1/3)*(9/4)*(-72/7)-(1/3)*51)==(-36/7)+(54/7)-17=
(54-36-119)/7=-101/7;
подставим х= 72/7 в правую часть исходного уравнения. получим
2*(-72/7)-(1/2)*(-72/7)+1=(-144+36+7)/7=-101/7
Решение верно.
ответ х= -10 2/7
1. у=4х-2
1)
х=0 у=4*0-2=-2
х=6 у=4*6-2=10
2)
у=0
4х-2=0
4х=2
х=0,5
у=2
4х-2=2
4х=4
х=1
2.
Пересечение с осью ОХ:
у=0
1,2х-24=0
1,2х=24
х=20
(20; 0)
Пересечение с осью ОУ:
х=0
у=1,2*0-24
у=-24
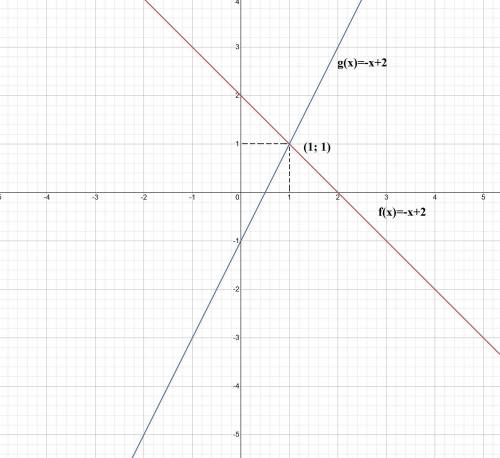
3. Поскольку оба графика линейные функции, то для построения достаточно 2х точек:
f(x)=-x+2
x y
0 2
1 1
g(x)=2x-1
x y
0 -1
2 3
1) Из графика видно, что точка пересечения (1; 1)
2) Из построенных графиков видно, что g(x)>f(x), при х>1.
4. График линейной функции имеет вид:
у=kx+b
a График проходит через точки (0; 0), (1; 1)
0=k*0+b ⇒b=0
1=k*1 ⇒k=1
у=х
б) Графиком является постоянная функция:
у=-2
в) График проходит через точки (0; 3) и (3;0)
3=0*k+b ⇒b=3
0=3k+b
3k=0-3
k=-1
y=-x+3
б) =3^x+3*3^x=4
]3^x=t
t+3t=4
4t=4
t=1
3^x=1
X=0
в) ...
]5^x=t
t^2 - 6*t +5=0
D=(-6)^2- 4*5
D=36- 20= 16
t=(6-4)/2=1 и t=(6+ 4)/2=5
5^x=1 5^x=5
X=0 x=1
в) ...
2^x>4^-1
2^x>2^-2
x>-2
И возможно здесь будет ответ от -2 до + бесконечности. Хотя, если честно я не уверена до конца, но если оно так то этот период записыаается в круглых скобках