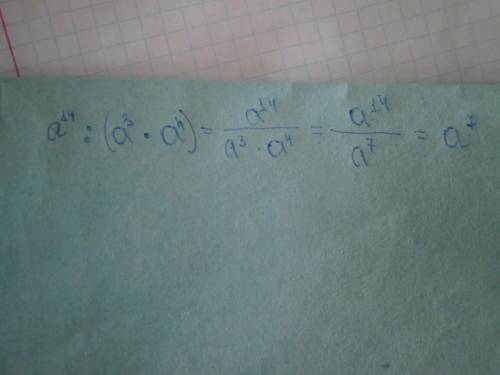
ответ: 4см и 13см
Объяснение: пусть ширина=х, а длина=у. Так как периметр =34см, составим уравнение: 2х+2у=34. Диагональ прямоугольника делит его на 2 прямоугольных треугольника в котором диагональ является гипотенузой и равна 13см. Составим на основании теоремы Пифагора уравнение: х²+у²=13². У нас теперь есть 2 уравнения для системы:
{2х+2у=34 |÷2
{х²+у²=13²
{х+у=17
{х²+у²=169
{х=17-у
{х²+у²=169
Теперь подставим значение х во 2-е уравнение: х²+у²=169:
(17-у)²+у²=169
289-34у+у²-169=0
у²-34у+120=0
D=1156-4×120=676
y1=(34-26)÷2=8÷2=4
y2=(34+26)÷2=60÷2=30. Итак:
у1=4
у2=30. Теперь подставим каждое значение у в уравнение х=17-у:
1) х=17-4=13см;
2) х=17-30= -13. Это второе значение нам не подходит, поскольку сторона не может быть отрицательной, поэтому мы берём для решения: у1=4. Тогда стороны прямоугольника: 4см и 13см
Р = 99 кПа = 99000 Па.
Ратм = 101 кПа = 101000 Па.
g = 10 Н/кг.
ρ = 1,2 кг/м3.
h - ?
Барометр показывает гидростатическое давление столба воздуха. Гидростатическое давление газа определяется формулой: P = ρ * g * h. Где ρ - плотность газа, g - ускорение свободного падения, h - высота столба газа, в нашем случае воздуха.
Ратм - Р = ρ * g * h1 - ρ * g * h2 = ρ * g * (h1 - h2), где h1 - высота столба воздуха над взлётной полосе, h2 - высота воздуха над вертолётом.
Высота полёта вертолёта h и есть разностью высот: h = h1 - h2.
h = (Ратм - Р) / ρ * g.
h = (101000 Па - 99000 Па) /1,2 кг/м3 * 10 Н/кг = 166,7 м.
ответ: вертолёт летит на высоте h = 166,7 м над поверхностью взлётной полосы.
Объяснение:
2) A^14 : A^7 = A^7
ответ A^7