ответ: а² > a⁴ .
Объяснение:
Так как на чертеже а² лежит на оси правее, чем а³ , то а² > а³ .
А это значит, что число "а" находится в пределах от 0 до 1: 0<a<1 .
Если , например, а=0,1 , то а²=0,01 , а³=0,001 , a⁴=0,0001 , то есть 0,0001<0,001<0,01<0,1 ⇒ a⁴ < a³ < a² < a .
Значит, и более старшие степени числа "а" будут давать меньшие значения. То есть а⁴ < a²
Для сравнения, если a>1 , то a⁴>a³>a²>a . Например, а=3 , тогда a⁴=81 , а³=27 , а=9 .
P.S. Самая крайняя левая точка на чертеже - это 0 , а не а .
ответ: а² > a⁴ .
Объяснение:
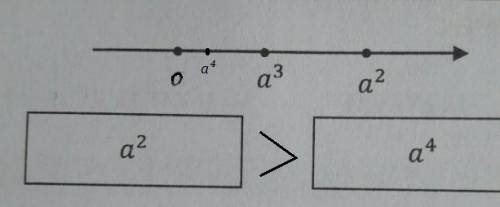
Так как на чертеже а² лежит на оси правее, чем а³ , то а² > а³ .
А это значит, что число "а" находится в пределах от 0 до 1: 0<a<1 .
Если , например, а=0,1 , то а²=0,01 , а³=0,001 , a⁴=0,0001 , то есть 0,0001<0,001<0,01<0,1 ⇒ a⁴ < a³ < a² < a .
Значит, и более старшие степени числа "а" будут давать меньшие значения. То есть а⁴ < a²
Для сравнения, если a>1 , то a⁴>a³>a²>a . Например, а=3 , тогда a⁴=81 , а³=27 , а=9 .
P.S. Самая крайняя левая точка на чертеже - это 0 , а не а .

составим уравнение: х*y = 12
А зная длину диагонали по теореме Пифагора получаем: х² + y² = 25
Итак имеем систему:
х*y = 12
х² + y² = 25
y = 12/х
х² + (12/х)² = 25
Решаем второе уравнение системы:
х² + 144/х² = 25 | *х²
х^4 + 144 - 25х² = 0
Замена: х² = t , t > 0
t² - 25t + 144=0
D = 625 - 4*144 = 625 - 576 = 49
t1 = (25+7)/2 = 16
t2 = (25-7)/2 = 9
х² = 16 или х² = 9
х = 4 х = 3
Тогда y = 12/4 = 3 или y = 12/3 = 4
ответ: стороны прямоугольника 3 и 4 .