Пусть х км расстояние, которое проехал велосипедист до встречи. Тогда мотоциклист проехал до встречи (80 - х) км. Так как велосипедист приехал в В через 3 часа после встречи, то он проехал расстояние (80 - х) км за 3 часа, а значит его скорость (80 - х)/3 (км/ч). Мотоциклист же расстояние х км проехал за 1 ч.20мин., т.е. за 4/3 часа, поэтому его скорость х: 4/3 = 3х/4 (км/ч). Так как до встречи они затратили одинаковое время, то можно составить уравнение:
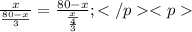
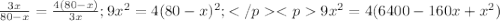
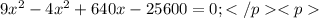
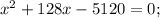
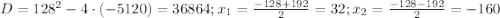
Так как за х мы брали расстояние от А до места встречи, то х = 32 (км).
ответ: На расстоянии 32 километра от пункта А произошла встреча.
1) Разложим знаменатели в дробях на множители:
а²-4а+4 = (а-2)²
а²-4 = (а-2)(а+2)
2) Отметим, что т.к. деление на 0 запрещено, то а не должно быть равно -2 и 2
3) домножим обе части уравнения на (а-2)*(а-2)*(а+2):
(а-2)(а-2)(а+2) / (а-2)² - 4*(а-2)(а-2)(а+2)/ ((а-2)(а+2)) = (а-2)(а-2)(а+2) / (а+2)
сократим дроби, получим: (а+2) - 4(а-2) = (а-2)(а-2)
перенесем все налево, раскроем скобки:
а+2-4а+8-а²+4а-4=0
а²-а-6=0
4) найдем корни уравнения, разложим на множители:
(а+2)(а-3)=0
вспомним, что а≠-2, значит, у нас будет только 1 корень:
ответ: а = 3
320/4=80
ответ: 80%