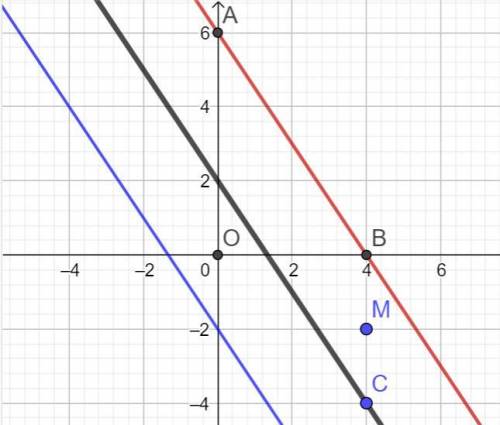
1) Уравнение 3х + 2у = 4 выразим относительно у:
у = (-3/2)х + 2.
Для симметричная прямой 3х+2у=4 в виде у = (-3/2)х + 2 относительно начала координат свободный член поменяет свой знак на противоположный.
ответ: уравнение у = (-3/2)х - 2 или в общем виде 3х - 2у + 4 = 0.
2) Найдём разность координат по у между точкой М и заданной прямой при х = 4 (как у точки М).
у(С) = (-3/2)*4 + 2 = -6 + 2 = -4.
Разность равна -4 - (-2) = -2.
Симметричная точка В получит приращение по у с обратным знаком:
у(В) = -2 + 2 = 0. Значит координаты точки В(4; 0).
Аналогично получаем точку А на оси Оу с учётом двукратного приращения: А(2 + 2*2 = 6; 0) = (6; 0).
По двум точкам находим уравнение симметричной прямой:
х/4 = (у - 6)/(-6) или -3х - 2у + 12 = 0.
ответ: уравнение прямой -3х - 2у + 12 = 0.
9X^2 + 24X - 4X + 16 - 12 = 0
9X^2 + 20X + 4 = 0
D = 400 -4*9*4 = 400 - 144 = 256
V D = 16
X1 = ( - 20 + 16 ) : 18 = ( - 4) : 18 = ( - 2\9 )
X2 = ( - 36 ) : 18 = ( - 2 )
ответ при Х = ( - 2\9) и ( - 2 )