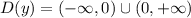
 получается с растягивания графика
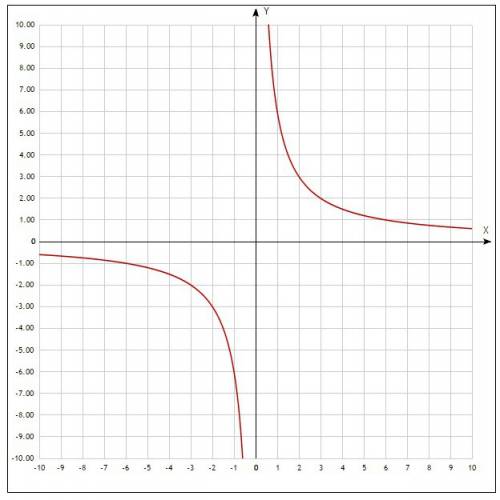
получается с растягивания графика 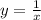 (обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности.
(обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности. тоже является гиперболой.
тоже является гиперболой.
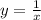 принимает отрицательные значения на луче
принимает отрицательные значения на луче 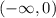 то и
то и  принимает отрицательные значения на луче
принимает отрицательные значения на луче 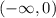
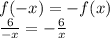

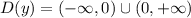
 получается с растягивания графика
получается с растягивания графика 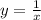 (обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности.
(обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности. тоже является гиперболой.
тоже является гиперболой.
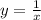 принимает отрицательные значения на луче
принимает отрицательные значения на луче 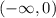 то и
то и  принимает отрицательные значения на луче
принимает отрицательные значения на луче 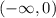
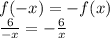


х=(4+у)
(4+у)²-2у=11
16+8у+у²-2у-11=0
у²+6у+5=0
По теореме Вието
у1+у2=-р=-6
у1*у2=q=5
y1=-1
y2=-5
x1=(4+y1)=4+(-1)=4-1
x1=3
x2=(4+y2)=4+(-5)=4-5
x2=-1
(3;-1) и (-1;-5)
y²+6y+5=0
D=(-6)²-4×1×5=36-20=16
y1=((-6)-√16)/2×1=(-6-4)/2=(-10)/2=-5
y2=((-6)+√16)/2×1=(-6+4)/2=(-2)/2=-1.