Объяснение:
№1
а) х2+5х-6=0
Д=b2-4ac=25-4*1*(-6)=25+24=49
б) 4х2-5х-4=0
Д=b2-4ac=25-4*4*(-4)=25+64=89
№2
а)х2-8х-84=0
Д=b2-4ac=64-4*1*(-84)=400.
Так как дискриминант положительный то уравнение имеет два корня.
б)36х2-12х+1=0
Д=b2-4ac=144-4*36*1=0
Так как дискриминант =0 то уравнение имеет один корень.
в)х2+3х+24=0
Д=b2-4ac=9-4*1*24=-87
Так как дискриминант отрицательный уравнение корней не имеет.
№3
а)х2-5х+6=0
Д=b2-4ac=25-4*1*6=1 Корень квадратный из Дискриминанта=1
Х1=(-b+Корень квадратный из Дискриминанта)/2a=(5+1)/2=3
X2=(-b-Корень квадратный из Дискриминанта)/2a=(5-1)/2=2
б)х2-2х-15=0
Д=b2-4ac=4-4*1*(-15)=64 Корень квадратный из Дискриминанта=8
Х1=(-b+Корень квадратный из Дискриминанта)/2a=(2+8)/2=5
X2=(-b-Корень квадратный из Дискриминанта)/2a=(2-8)/2=-3
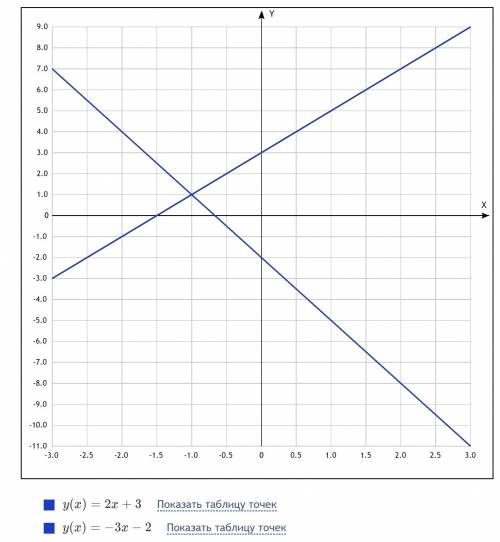
2x - y = -3; <=> y = 2x + 3. (1)
3x + y = -2; <=> y = -3x - 2. (2)
Построим графики функций (1) и (2). Координаты точки их пересечения и будут решением системы.
Функции (1) и (2) линейные, то есть их графиками являются прямые. Для построения прямой достаточно двух точек.
Строим график функции (1): при x = 0 y = 3; при x = 1 y = 5. Через точки (0, 3) и (1, 5) проводим прямую.
Строим график функции (2): при x = 0 y = -2; при x = -1 y = 1. Через точки (0, -2) и (-1, 1) проводим прямую.
По чертежу очевидно, что графики функций (1) и (2) пересекаются в точке (-1, 1). Следовательно, (-1, 1) - решение системы.
ответ: (-1, 1).
Чертеж:
2х+3=0
2х=-3
х=-1,5