Question

Существует ли точка, лежащая на графике функции , ордината которой равна: 1)-4; 2)-2,5; 3)0; 4)1; 5)3 ? если существует, то найдите её координаты.

Answer 1

1) Подставим у=-4 в график уравнения, получим

$-4=-x^2+x+2\\ x^2-x-6=0$

По теореме Виета

$x_1=3;~~~ x_2=-2$

Координаты: (-2;-4), (3;-4).

2) Аналогично, подставляем y=-2.5 в график уравнения, имеем

$-2.5=-x^2+x+2\\ x^2-x-4.5=0\\D=(-1)^2-4\cdot1\cdot(-4.5)=19\\ \\ x_{1,2}=\dfrac{1\pm\sqrt{19}}{2}$

Координаты: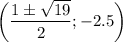 $\bigg(\dfrac{1\pm\sqrt{19}}{2};-2.5\bigg)$

3) Подставляем y=0 в график уравнения, получим

$0=-x^2+x+2=0\\ x^2-x-2=0$

По теореме Виета:

$x_1=-1;~~~ x_2=2$

Координаты: (-1;0), (2;0).

4) Подставим y=1 в заданный график уравнения, имеем

$1=-x^2+x+2\\ x^2-x-1=0\\D=(-1)^2-4\cdot1\cdot(-1)=5\\ \\ x_{1,2}=\dfrac{1\pm\sqrt{5}}{2}$

Координаты: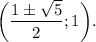 $\bigg(\dfrac{1\pm\sqrt{5}}{2};1\bigg).$

5) И наконец-то подставляем y=3 в график уравнения, имеем:

$-x^2+x+2=3\\ x^2-x+1=0\\D=(-1)^2-4\cdot1\cdot1=-3<0$

Так как D<0, то квадратное уравнение действительных корня не имеет, значит и не существуют точки.