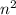коэффициент положительный, ветви параболы смотрят вверх, следовательно больше нуля заштрихованная область.
S= n(n+1)/2= 243k= 3^5*k.
n(n+1)= 2*243k= 486k= 2*3^5*k.
Значит, нужно найти два последовательных натуральных числа, произведение которых должно быть делимо и на 2 (т. е. одно из них д. б. чётным, что всегда соблюдается) и на 3^5. Если оно из чисел делится на 3, то соседние ему числа не делятся на 3. Следовательно, одно из чисел обязательно должно быть делимо на 3^5= 243. Наименьшее из таких чисел: 243. Рядом с ним есть два числа: 242 и 244. Выбираем меньшее из них: 242. Таким образом, n= 242.
е)у=-х^2+3
Объяснение:
на самом деле ничего сложного в решении нет , через точку может проходить бесконечное количество различных функций, поэтому мы просто должны перебрать варианты которые нам даны , для начала вид записи точки это T(x,y) ,где T это название точки(оно не обязательно) , x y координаты точки , теперь просто подставляем в наши уравнения
вместо x -1 вместо y 2
а)2=-5(-1)+2=7 не подходит
в)2=(-1)^2+3=4 не подходит
д)2=5(-1)+3=-2 не подходит
e)2=-((-1)^2)+3=2 подходит