ответ: 65 км/ч
Объяснение:
1) 312 : 2 = 156 (км) - половина расстояния
2) 12 мин = 12/60 ч = 1/5 ч
Скорость Время Расстояние
До остановки x - 5 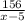 156
156
После ост. x 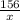 156
156
Время до остановки на 12 мин больше времени после остановки:
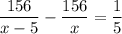
х > 5 по смыслу задачи, поэтому умножим обе части уравнения на
5x(x - 5):
780x - 780(x - 5) = x(x - 5)
780x - 780x + 3900 = x² - 5x
x² - 5x - 3900 = 0
По теореме Виета:
x₁ · x₂ = - 3900
x₁ + x₂ = 5
Значит, x₁ = - 60 - не подходит по смыслу задачи
x₂ = 65
ответ: 65 км/ч
Предлагаю для начала решить уравнение:
(3x² + 2x - 1)/(x + 1) = 5
ОДЗ: x + 1 ≠ 0
x ≠ -1
(3x² + 2x - 1)/(x + 1) * (x + 1) = 5 * (x + 1)
3x² + 2x - 1 = 5 * (x + 1)
3x² + 2x - 1 = 5x + 5
3x² + 2x - 5x - 1 - 5 = 0
3x² - 3x - 6 = 0
D = (-3)² - 4 * 3 * (-6) = 9 + 72 = 81
x₁,₂ = (3 ± √81)/(2 * 3) = (3 ± 9)/6
x₁ = (3 + 9)/6 = 12/6 = 2
x₂ = (3-9)/6 = -6/6 = -1 (посторонний корень, не соответствует ОДЗ).
ОТВЕТ: x = 2.
Отвечаю на Ваш вопрос.
В дробно-рациональных уравнениях (подобных данному) нужно избавляться от знаменателя. Он никуда автоматически не пропадает. Просто все уравнение имеют такую особенность, что если умножить обе чести уравнения на одно и то же число (или выражение), то корни уравнения остаются прежними. В таком случае чтобы "исчез" знаменатель (то есть чтобы от него избавиться) обе части уравнения умножают на общий знаменатель (вторая строчка решения, не учитывая ОДЗ).
q=1/2
S6=(b1(q^n-1))/(q-1)=(8(1/64-1))/(1/2-1)=(8(-63/64))/(-1/2)=63/8 *2=63/4=15.75