
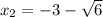
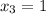

Объяснение:
(x² + 6x)² - 4(x² + 6x + 1) - 17 = 0
t = (x² + 6x)
t² - 4(t + 1) - 17 = 0
t² - 4t - 4 - 17 = 0
t² - 4t - 21 = 0
t² + 3t - 7t - 4 - 17 = 0 (Теорема Виета)
t² + 3t - 7t - 21 = 0
t(t + 3) - 7(t + 3) = 0
(t + 3)(t - 7) = 0
t₁ = -3; t₂ = 7
x² + 6x + 3= 0 x² + 6x - 7 = 0
D = b² - 4ac D = b² - 4ac
D = 6² - 4 * 1 * 3 D = 6² - 4 * 1 * (-7)
D = 36 - 12 D = 36 + 28
D = 24 D = 64
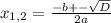



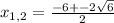

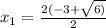

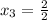
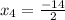

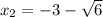
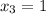

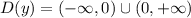
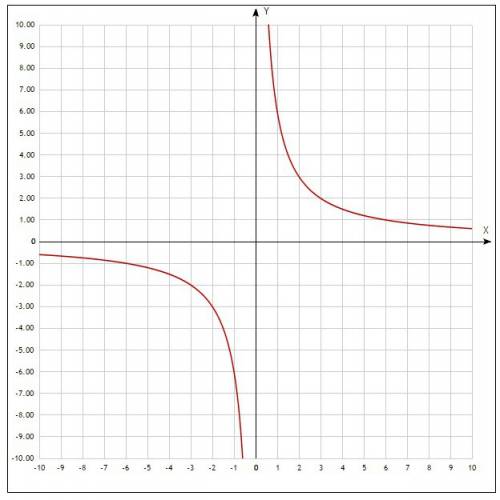
 получается с растягивания графика
получается с растягивания графика 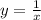 (обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности.
(обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности. тоже является гиперболой.
тоже является гиперболой.
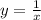 принимает отрицательные значения на луче
принимает отрицательные значения на луче 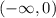 то и
то и  принимает отрицательные значения на луче
принимает отрицательные значения на луче 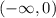
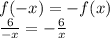

б)t^2-18t+81=(t+9)^2
3)4c^2+2*2c*3/4d+9/16d^2=(2c+3/16d)^2 ...2*2c*3/4d=3*c*d
4)