По формуле:
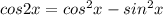
Зная это получаем:
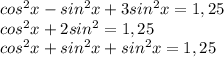
Известно что:
отсюда получаем:
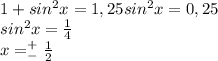
Получаем 2 уравнения:
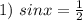это табличное значение синуса и получается 2 решения:
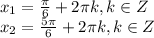
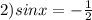аналогично получаем 2 решения:
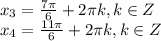
Теперь обратим внимание, что эти 4 решения можно записать в 2 решения в виде:
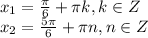
Теперь надо найти при каких значениях k и n решения лежат на отрезке ![[0; \frac{5\pi}{2}]](/tpl/images/0071/0603/9e0ce.png)
Для этого решаем 2 неравенства
1) 
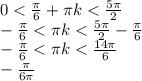
Так как к у нас принадлежит целым числам, то получается что к=0,1,2
2) Теперь ищем n, аналогично:
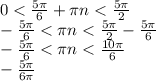
Поскольку n принадлежит целым числам, то получается что n=0,1
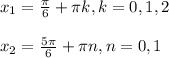
Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
y=-10-наименьшее