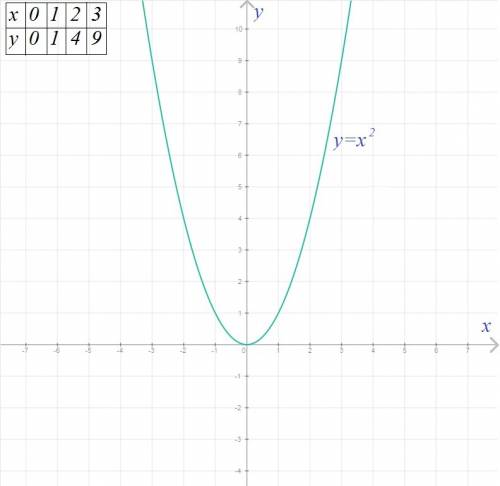
График функции y=x² на картинке.
ТЕОРИЯ (читать всем!):
Чтобы узнать, принадлежит ли точка графику функции, нужно подставить в уравнение графика данные нам координаты точки.
Теперь смотрим: если уравнение обращается в верное равенство, значит, точка принадлежит графику; если нет, то точка не принадлежит графику функции.
Координата точки — А(x;y)
а) A(-10;-100). Подставим координату в уравнение графика функции y=x²:
-100 = (-10)²
-100 = (-10)·(-10)
-100 ≠ 100
Значит, точка А(-10;-100) не принадлежит графику функции y=x².
ответ: не принадлежит.
б) B(8;64). Подставим координату в уравнение графика функции y=x²:
64 = 8²
64 = 8·8
64 = 64
Значит, точка B(8;64) принадлежит графику функции y=x².
ответ: принадлежит.
в) С(-6;36). Подставим координату в уравнение графика функции y=x²:
36 = (-6)²
36 = (-6)·(-6)
36 = 36
Значит, точка C(-6;36) принадлежит графику функции y=x².
ответ: принадлежит.
точка A(-10;-100) — не принадлежит графику функции.
точка B(8;64) — принадлежит графику функции.
точка С(-6;36) — принадлежит графику функции.
5(4a^2-9b^2)
5(2a-3b)(2a+3b)
2) 128a^3b-2ab^3
2ab(64a^2-b^2)
2ab(8a-b)(8a+b)
3) x^4-y^4
(x^2-y^2)(x^2+y^2)
(x-y)(x+y)(x^2+y^2)
4) x^8-y^8
(x^4-y^4)(x^2+y^2)
(x^2-y^2)(x^2+y^2)(x^2+y^2)
(x-y)(x+y)(x^2+y^2)(x^2+y^2)
5) a^4-1
(a^2-1)(a^2+1)
(a-1)(a+1)(a^2+1)
6) 1-81y^4
(1-9y^2)(1+9y^2)
(1-3y)(1+3y)(1+9y^2)