1. -15 ≤ 1-2у ≤ 0
2. 
Объяснение:
1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
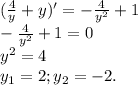
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2: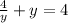 
.
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
для у=1/2 :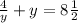 
для у=8: .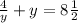
Т.е. имеем кривую с максимумами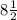 
и минимумом 4.
Тогда
Слева - график модуля, это "галочка".
Основание в точке х=5.
Справа - прямая, параллельная оси Ох, проходящая через точку (0; a^2 + 1).
Корни = точки пересечения двух графиков. Одинаковых знаков = либо положительные, либо отрицательные.
Судя по нашему графику, точек пересечения графика с прямой либо одна (x=5, a^2+1=5), либо две. Когда имеется две точки пересечения, то рассматриваем вариант, когда оба корня положительные. Это возможно, когда прямая пересечет график в точках x>0. Когда х=0, y=5. Получаем неравенство: 0< a^2 + 1< 5
-1<a^2<4, -2<a<2
ответ: -2<a<2 (вариант, когда графики имеют одну общую точку не рассматриваем, т.к. условие требует наличие более одного корня)