a_1,\ a_1+d,\ a_1+2d,\ \ldots,\ a_1+(n-1)d, \ \ldots Так что ~n-й член арифметической прогрессии равен ~{a_n}={a_1}+{ \left( n-1 \right) }d Более точно: последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d (шага или разности прогрессии). Иначе говоря, для всех элементов прогрессии, начиная со второго, выполнено равенство: a_n=a_{n-1} + d \quad Любой член прогрессии может быть вычислен по формуле: a_n=a_1 + (n-1)d \quad \forall n \ge 1 (формула общего члена) Шаг прогрессии может быть вычислен по формуле: d=\frac{a_n-a_m}{n-m}, если n\neq m Если шаг d > 0, прогрессия является возрастающей; если d < 0, — убывающей.
Если вписать квадрат в окуржность, то его диагональ будет диаметром этой окружности (угол опирающийся на диаметр - прямой). Таким образом длина диагонали квадрата вписанного в окружность: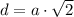 
, где a - сторона квадрата. Так как диагональ есть диаметр то она равна двум радиусам: 
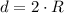. Тогда выразим длину стороны квадрата: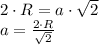 
Если вписать окружность в квадрат, то ее радиус будет равен половине стороны квадрата: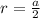 
. Подставив предыдущую формулу в данную, получим: 
.
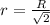Таким образом мы получили бесконечно убывающую геометрическую прогрессию радиусов окружностей. Первый элемент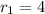 
, знаменатель прогресии 
.
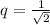Сумма всех радиусов равна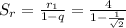 
.
Тогда сумма длин всех окружностей: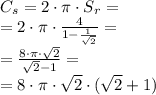 
2x-x=0
x-0
x=0:1
x=0
2) y^2-4y=0
2y-4y=0
-2y=0
y=-0:2
y=-0
3) 2y(9y-6)+5(6-9y)=0
18y^2-12y+30-45=0
36y-12y=0-30+45
24y=15
y=15:24
y=