20(x²-6x-9)²=x(x²-4x-9)
(x²-6x-9)²-x(x²-4x-9)=0
(x²-6x)²-2(x²-6x)·9+9²-x³+4x²+9x=0
x⁴-12x³+36x²-18x²+108x+81-x³+4x²+9x=0
x⁴-13x³+22x²+117x+81=0
подставив вместо х=-1 убеждаемся, что 1+13+22-117+81=0 - верно
Значит х=-1 - корень данного уравнения
Делим x⁴-13x³+22x²+117x+81 на (х+1)
получим х³-14х²+36х+81
Итак,
x⁴-13x³+22x²+117x+81=(х+1)·(х³-14х²+36х+81)
корни многочлена
х³-14х²+36х+81
следует искать среди делителей свободного коэффициента 81
Это числа ±1;±3;±9
Подставим х=9 и убеждаемся, что 9³-14·9²+36·9+81=81(9-14+4+1)=81·0=0
х=9 - корень данного уравнения
х³-14х²+36х+81 делим на (х-9)
получим х²-5х-9
Осталось разложить на множители последнее выражение
х²-5х-9=0
D=25+36=61
x=(5-√61)/2 или х=(5+√61)/2
Окончательно
x⁴-13x³+22x²+117x+81=0 ⇒(х+1)·(х³-14х²+36х+81)=0⇒(х+1)(х-9)(х²-5х-9)=0⇒ х₁=-1 или х₂=9 или x₃=(5-√61)/2 или х₄=(5+√61)/2
Объяснение:
;
;
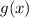и будет искомой фигурой.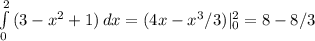
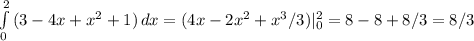
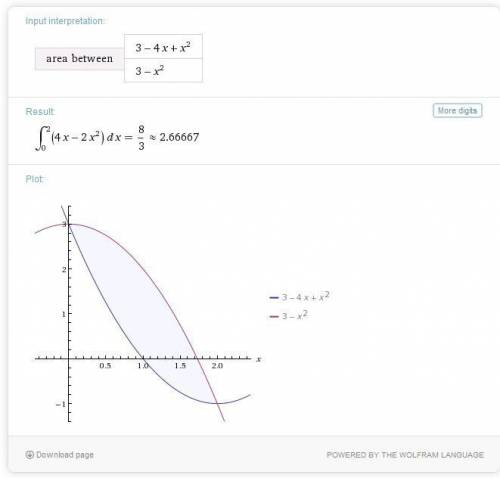
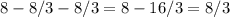(кв. ед.)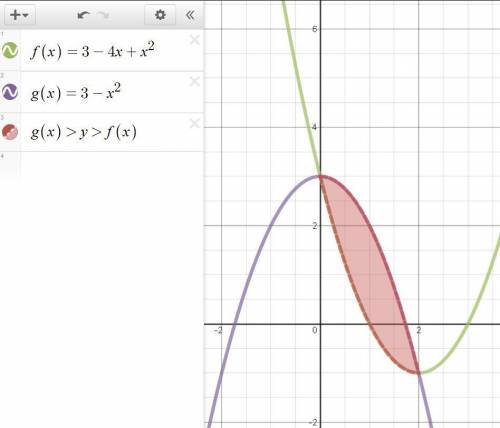
2 - 18cos⁴(π-x).