1. Всего карточек 50 из них 9; 18; 27; 36; 45 кратны 9 - их всего 5 карточек.
Всего все возможных событий: n=50
Всего благоприятных событий: m = 5
Искомая вероятность: P = m/n = 5/50 = 1/10 = 0,1.
2. Всего все возможных подбрасывания игральных кубиков: 6*6=36
На желтой кости выпало четное число: {2;4;6}
На красной кости - {5}
Всего благоприятных событий: 3*1 = 3.
Искомая вероятность: P = 3/36 = 1/12
3. Вероятность того, что вынутая наугад карта окажется шестеркой красной масти равна . Тогда вероятность того, что вынутая наугад карта окажется не шестеркой красной масти равна
4. Выпишем все выпадения очков, в сумме не меньше 11.
{6;6}, {5;6}, {6;5} - всего 3
Искомая вероятность: P = 3/36 = 1/12
5. Всего все возможных событий:
Один красный шар можно достать а один белый По правилу произведения, достать один красный и один белый шары можно
x^2-2x-12+3x^2-6x-13=0 Произведем замену переменных. Пусть t=x^2-2x В результате замены переменных получаем вс уравнение. 3t-13+t^2-2t+1=0 Раскрываем скобки. 3t-13+t^2-2t+1=0 3t-13+1+t^2-2t=0 3t-12+t^2-2t=0 Приводим подобные члены. 1t-12+t^2=0 t-12+t^2=0 Изменяем порядок действий. t^2+t-12=0 Находим дискриминант. D=b^2-4ac=12-4•1-12=49 Дискриминант положителен, значит уравнение имеет два корня. Воспользуемся формулой корней квадратного уравнения. t1,2=-b±D/2a t1=-1-72•1=-4 ;t2=-1+72•1=3 ответ вс уравнения: t=-4;t=3 . В этом случае исходное уравнение сводится к уравнению x^2-2x=-4 ;x^2-2x=3 Теперь решение исходного уравнения разбивается на отдельные случаи. Случай 1 . x^2-2x=-4 Перенесем все в левую часть. x^2-2x+4=0 Находим дискриминант. D=b^2-4ac=-22-4•1•4=-12 Дискриминант отрицателен, значит уравнение не имеет корней. Итак,ответ этого случая: нет решений. Случай 2 . x^2-2x=3 Перенесем все в левую часть. x^2-2x-3=0 Находим дискриминант. D=b^2-4ac=-22-4•1-3=16 Дискриминант положителен, значит уравнение имеет два корня. Воспользуемся формулой корней квадратного уравнения. x1,2=-b±D/2a x1=2-42•1=-1 ;x2=2+42•1=3 Итак,ответ этого случая: x=-1;x=3 . Окончательный ответ: x=-1;x=3 .
1. Всего карточек 50 из них 9; 18; 27; 36; 45 кратны 9 - их всего 5 карточек.
Всего все возможных событий: n=50
Всего благоприятных событий: m = 5
Искомая вероятность: P = m/n = 5/50 = 1/10 = 0,1.
2. Всего все возможных подбрасывания игральных кубиков: 6*6=36
На желтой кости выпало четное число: {2;4;6}
На красной кости - {5}
Всего благоприятных событий: 3*1 = 3.
Искомая вероятность: P = 3/36 = 1/12
3. Вероятность того, что вынутая наугад карта окажется шестеркой красной масти равна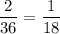 . Тогда вероятность того, что вынутая наугад карта окажется не шестеркой красной масти равна
. Тогда вероятность того, что вынутая наугад карта окажется не шестеркой красной масти равна 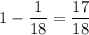
4. Выпишем все выпадения очков, в сумме не меньше 11.
{6;6}, {5;6}, {6;5} - всего 3
Искомая вероятность: P = 3/36 = 1/12
5. Всего все возможных событий: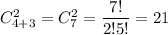
Один красный шар можно достать а один белый По правилу произведения, достать один красный и один белый шары можно
Искомая вероятность: P = 12/21 = 4/7