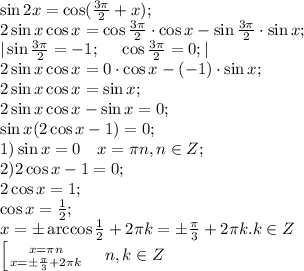
![x\in(\frac{4\pi}{3};4\pi]=(\pi+\frac{\pi}{3};4\pi]\\ 1) x=\pi n;\ \ \\ n=1:x=\pi\notin(\frac{4\pi}{3};4\pi];\\ n=2:x=2\pi\in(\frac{4\pi}{3};4\pi];\\ n=3:x=3\pi\in(\frac{4\pi}{3};4\pi];\\ n=4:x\in(\frac{4\pi}{3};4\pi];\\ n=5:x\notin(\frac{4\pi}{3};4\pi];\\](/tpl/images/0245/3660/ec711.png)
![2) x=\pm\frac{\pi}{3}+2\pi k;\\ k=0:x=\pm\frac\pi3\notin(\frac{4\pi}{3};4\pi];\\ k=1: x=\pm\frac{\pi}{3}+2\pi= \left[ {{x=\frac{5\pi}{3}\in(\frac{4\pi}{3};4\pi];\\} \atop {x=\frac{7\pi}{3}\in(\frac{4\pi}{3};4\pi];\\}} \right. \\ k=2:x=\pm\frac\pi3+4\pi= \left[ {{x=\frac{11\pi}{3}\in(\frac{4\pi}{3};4\pi]} \atop {x=\frac{13\pi}{3}\notin(\frac{4\pi}{3};4\pi]}} \right. ](/tpl/images/0245/3660/d791d.png)
![2) x=\pm\frac{\pi}{3}+2\pi k;\\ k=0:x=\pm\frac\pi3\notin(\frac{4\pi}{3};4\pi];\\ k=1: x=\pm\frac{\pi}{3}+2\pi= \left[ {{x=\frac{5\pi}{3}\in(\frac{4\pi}{3};4\pi];\\} \atop {x=\frac{7\pi}{3}\in(\frac{4\pi}{3};4\pi];\\}} \right. \\ k=2:x=\pm\frac\pi3+4\pi= \left[ {{x=\frac{11\pi}{3}\in(\frac{4\pi}{3};4\pi]} \atop {x=\frac{13\pi}{3}\notin(\frac{4\pi}{3};4\pi]}} \right. \\ x=\frac{5\pi}{3};\ \ 2\pi;\ \ \frac{7\pi}{3};\ \ 3\pi;\ \ \frac{11\pi}{3};\ \ 4\pi](/tpl/images/0245/3660/64a96.png)
Раскладывать выражения на множители будем, используя группировки:
1). x – 3y + x2 – 9y2 = (x – 3y) + (x2 – 9y2).
По формуле а2 – b2 = (a – b)(а + b):
(x – 3y) + (x – 3y)(x + 3y).
Выносим выражение (x – 3y) за скобку:
(x – 3y)(1 + x + 3y).
2). 9m2 + 6mn + n2 – 25 = (9m2 + 2 ∙ 3mn + n2) – 25.
Упростим выражение в скобках по формуле квадрат суммы (а + b)2 = (а2 + 2ab + b2) и раскладываем как разность квадратов:
(3m + n)2 – 52 = (3m + n – 5)(3m + n + 5).
3). Выносим b3 за скобку и группируем:
ab5 – b5 – ab3 + b3 = b3(ab2 – b2 – a + 1) = b3((ab2 – b2) – (a – 1)) = b3[b2(a – 1) – (a – 1)].
Выносим общий множитель (a – 1) за скобку:
b3(a – 1)(b2 – 1).
4). 1– x2 + 10xy – 25y2 = 1– (x2 – 10xy + 25y2).
Выражение в скобке «сворачиваем» как квадрат разности, к полученному выражению применяем формулу разности квадратов а2 – b2 = (a – b)(а + b):
1– (x – 5y)2 = (1– x + 5y)(1+ x – 5y).
ответ: 1). x – 3y + x2 – 9y2 = (x – 3y)(1 + x + 3y); 2). 9m2 + 6mn + n2 – 25 = (3m + n – 5)(3m + n + 5); 3). ab5 – b5 – ab3 + b3 = b3(a – 1)(b2 – 1); 4). 1– x2 + 10xy – 25y2 = (1– x + 5y)(1+ x – 5y).
Объяснение:
по формуле cos(3п/2+a)=-sina
cos(3п/2+x) =-sinx
sin2x=-sinx
2sinx*cosx=-sinx
разделим на sinx, при этом учитываем что корень уравнения sinx=0, тоже подходит
2cosx=-1
cosx=-1/2
x=arccos-1/2
x1=2п/3+2пn, n -целые числа и
x2=4п/3+2пn, n -целые числа
решая уравнение sinx=0, получаем, что x=пn, n -целые числа
из промежутка (4п/3 ; 4п] нам подходят 2п, 8п/3, 3п, 10п/3, 4п
ответ: 2п, 8п/3, 3п, 10п/3, 4п