Подкоренное выражение 7х - х² должно быть положительным или равным нулю, потому что извлекать квадратный корень из отрицательного числа нельзя.
7х - х² ≥ 0.
Решим неравенство методом интервалов. Найдем нули функции.
7х - х² = 0.
Вынесем за скобку общий множитель х.
х(7 - х) = 0.
Произведение двух множителей равно нулю тогда, когда один из множителей равен нулю.
1) х = 0;
2) 7 - х = 0;
х = 7.
Отметим на числовой прямой точки 0 и 7.
Эти числа делят числовую прямую на интервалы 1) (-∞; 0], 2) [0; 7], 3) [7; +∞).
Выясним, на каком из интервалов выражение 7х - х² будет принимать положительные значения. На 1 и 3 интервалах это выражение отрицательно, на 2 итервале - положительно. Поэтому, значения х, принадлежащие 2 интервалу являются областью определения функции.
ответ. [0; 7].
Объяснение:
1.
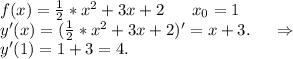
ответ: y'(1)=4.
2.

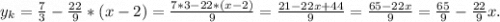
3.
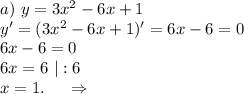
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(-∞;1) функция убывает.
При х∈(1;+∞) фунуция возрастает .
![b)\ y=x^9-9x\\y'=(x^9-9x)'=9x^8-9=9*(x^8-1)=0\\9*(x^8-1)=0\ |:9\\x^8-1=0\\x^8=1\\x=\sqrt[8]{1}\\x_1=-1\ \ \ \ x_2=1](/tpl/images/1848/3010/401ca.png)
В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума.
При х∈(-∞;-1) фунуция возрастает .
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(1;+∞) функция возрастает. ⇒
При х∈(-1;1) функция убывает.
никак не сократить