Выражения 1) -2ab^3*3a^2*5^4. 2) (-2a^5b^2)^3. - id248890520200722 от Йфячы 22.07.2020 22:54

Question

Алгебра: Выражения 1) -2ab^3*3a^2*5^4. 2) (-2a^5b^2)^3.

Йфячы · Accepted Answer

Пусть функция 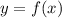y=f(x) определена на отрезке [a;b]

Разобьём отрезок произвольным образом на n частей точками:

$a < x_{0}$

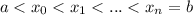
В каждом интервале произвольным образом выбираем точку

$c_{i}\in [x_{i-1};x_{i}]$

Cумма

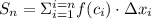$S_{n}=\Sigma^{i=n}_{i=1}f(c_{i})\cdot \Delta x_{i}$ ,

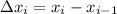где $\Delta x_{i}=x_{i}-x_{i-1}$ - длина частичного отрезка $[x_{i-1};x_{i}]$ ,

называется интегральной суммой функции 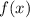f(x) на отрезке [a;b] .

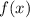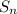Определенным интегралом от функции f(x) на отрезке [a;b] называется предел интегральных сумм $S_{n}$ , при условии, что длина наибольшего частичного отрезка стремится к нулю

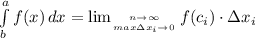
$\int\limits^a_b {f(x)} \, dx = \lim_{{ {{n \to \infty} \atop {max \Delta x_{i} \to 0}} \right. } f(c_{i})\cdot \Delta x_{i}$

Геометрическая интерпретация определённого интеграла - площадь криволинейной трапеции

Выражения 1) -2ab^33a^25^4. 2) (-2a^5b^2)^3.

MOGZ ответил