Объяснение:
15.6
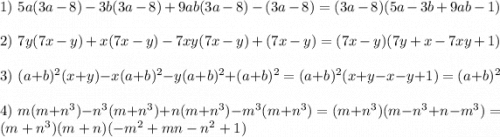
Выносим общую скобку как множитель.
15.9
Тут необходимо сначала разложить на множители, а затем воспользоваться правилом:
Если произведение двух или более множителей равно 0, то хотя бы один из множителей равен 0.
1)
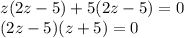
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
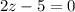 или
или 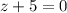
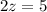 или
или 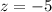
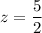 или
или 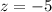
Мы решили! Это и есть ответ!
2)
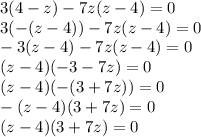
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
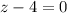 или
или 
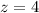 или
или 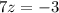
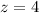 или
или 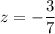
Мы решили! Это и есть ответ!
3)
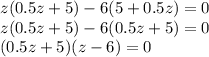
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
 или
или 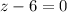
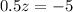 или
или 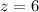
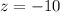 или
или 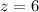
Мы решили! Это и есть ответ!
4)
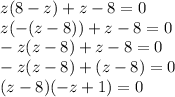
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
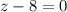 или
или 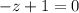
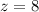 или
или 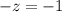
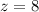 или
или 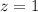
Мы решили! Это и есть ответ!
ну смотри.
Возьмём в пример это:
(а+4)(6+а)
Мы должны умножать дугой: а×6=6а, а×а=а², 4×6=24, 4×а=4а.
Я прикреплю фото, чтобы было понятнее.
ответом будет являться: 6а+а²+24+4а.
Но ответ не окончательный, убираем подобные: 6а и 4а.
ответ: 10а+а²+24.
Выражение в виде произведения многочленов.
Пример:
а(m-3)+b(m-3)
В данном случае общим множителем является многочлен m-3. Поэтому выносим его в начало, а множители за скобками складываем и умножаем;
(m-3)(a+b)
Метод группировки.
Метод группировки - это разложение многочлена на множители, объединив в группы его члены.
Пример:
2ас+2bc+5am+5bm
Сгруппировать члены этого многочлена нужно так, чтобы слагаемые в каждой группе имели общий множитель.
2ас+2bc+5am+5bm=(2ac+2bc)+(5am+5bm)=
=2c(a+b)+5m(a+b)=(a+b)(2c+5m).
Ничего сложного нет, нужно это только понять.)
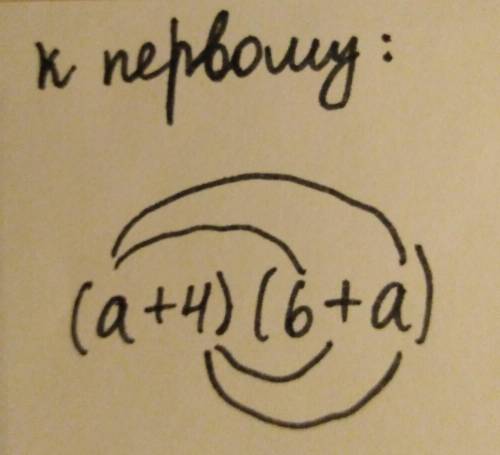
2. Если х ≠ 0, то у > 0, все точки параболы, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции у = х*2 является промежуток [0; + ∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны,парабола симметрична относительно оси ординат (функция у = х2 - четная).
5. На промежутке [0; + ∞) функция у=х*2 возрастает.
6. На промежутке (-∞; 0] функция у = х*2 убывает.
7. Наименьшее значение функция принимает в точке х = 0, оно равно 0.
8. Наибольшего значения не существует.