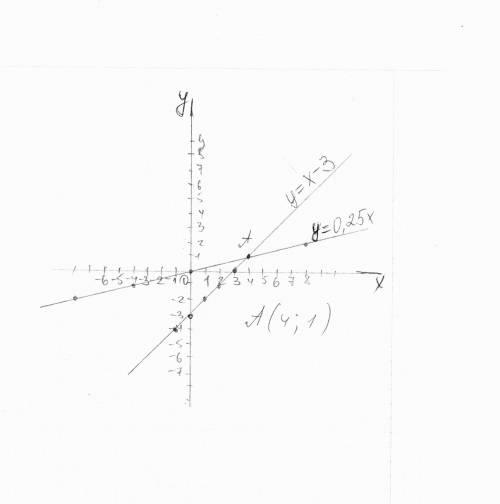
0,5х-2у=0 х-у-3=0
0,5х=2у у=х-3
у=0,25х
Теперь подставляем вместо х любое число,находим у и строим графики.Например:
0,25*0=0 (х=0,у=0)
0,25*4=1 (х=4,у=1) и т.д.
Так же и со вторым уравнением:
0-3=-3 (х=0,у=-3)
5-3=2 (х=5,у=2) и т.д.
Когда построите эти графики,они пересекуться в точке(4;1).Можно доказать это и по другому.Приравняем правые части наших уравнений:
0,25х=х-3
х-0,25х=3
0,75х=3
х=4
Подставим это значение в наши уравнения и найдем у:
0,25*4=1 и 4-4=1, т.е. у в обоих случаях=1
ответ: (4;1)
1) tg390° + cos840°- ctg135° + sin(-420°) =
= tg(390° - 360°) + cos(840°- 720°)- ctg (180°- 45°) - sin(420°- 360°) =
= tg 30° + cos 120°+ ctg 45° - sin 60° =
=√3/3 + cos (180° - 60°) + 1 - √3/2 =
=√3/3 - cos 60° + 1 - √3/2 =
=√3/3 - 1/2 + 1 - √3/2 =
= 1/2 - √3/6
2) cos 165° - tg75° =
= cos (90° + 75°) - tg75° =
= -sin 75° - sin 75°/cos75° =
= (-sin 75° · cos75° - sin 75°)/cos75° =
= (-0.5 sin 150° - sin 75°)/cos75° =
= (-0.5 sin (180°-30°) - sin (45°+30°)/cos(45°+30°) =
= (-0.5 sin 30° - sin 45°·cos30° - cos45°·sin30°)/(cos45°·cos 30°- sin45°·sin30°) =
= (-0.5 ·0.5 - 0.5√2 · 0.5√3 - 0.5√2 ·0.5)/(0.5√2·0.5√3- 0.5√2·0.5) =
= (-0.25 - 0.25√6 - 0.25√2 )/(0.25√6- 0.25√2) =
= -(1 + √6 + √2 )/(√6- √2) =
= -[(√6 + √2) + (√6 + √2)²]/(6- 2) =
= -[(√6 + √2) + (6 + 4√12 + 2)]/4 =
= -[√6 + √2 + 8 + 8√3]/4=
= -[√2(√3 +1) + 8(1 + √3]/4=
= -0.25[(√3 +1)(√2 + 8)]
3) sinx= - 0.5
x = -150°; -30°, 210°, 330°
Второй множитель просто добавляет к записи 7 нолей, рассматриваем первый множитель. 98 — "немного меньше" 100, поэтому было бы логично ожидать, что
Оценим
Используем неравенство Бернулли:
Итак, десятичная запись числа