а) y=(x-2) в 4 степени
1)Четная
2)Определена на всей области определения
3)Вершина в точке (2;0)
4)Ветви направлены вверх.
5)До x<2 убывает.
6)При x>4 возрастает.
б)0.5sinx+2
1) Определена на всей области определения
2) Нечетная
3) Периодическая
4) Возрастает и убывает
5) Знакопостоянна на промежутках
6) Непрерывна
7) График называеться синусойдой
в)y=0.5cosx+2
1)Определена на всей области определения
2)Четная
3)Периодическая
4)Область значений отрезок [ 1,5; 2,5];
5)Убывает на промежутках [KeZ; п+2пk] и возрастает на промежутках [п+2пk;KeZ]
Г)y=-(x+2)в 4 степени.
1)Определена на всей области определения
2) Вершина в точке (-2;0)
3)Возростает (-бесконечности;-2);
4)Убывает (-2;+бесконечности);
5)Ветви направлены в низ
6) Область значений (0;-бесконечности)
7) Ость оссимптот: x=-2
8)Наибольшее значение при y=0; x=-2
9) Наименьшего значения не существует
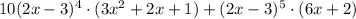
Объяснение:
Для начала необходимо понять, что данное выражение представляет собой произведение двух функций, а для производной от произведения функций существует правило:
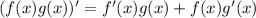
В данном случае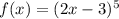 
, а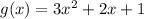 
Итак, нам потребуется производная от функции 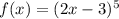, которая является сложной функцией, производная от которой берется по следующему правилу:
Здесь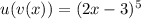 
, 
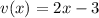
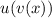- степенная функция, для нее правило такое:
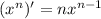
Вычисляем:
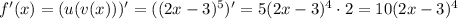
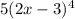мы получили, когда брали производную от внешней степенной функции , двойка появилась в результате взятия производной от 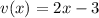. Т.е.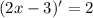 
---
Теперь возьмем производную от второго сомножителя в исходном выражении:
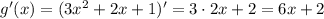
Подставляем все в формулу: ![\[(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\]](/tpl/images/1008/0917/ca526.png)
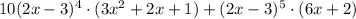
Чтобы функция убывала на всей числовой прямой, производная должна быть меньше нуля, поэтому
-3x² + 2px - 3 < 0, ⇒ 3x² - 2px + 3 > 0
т.е. диcкриминант должен быть меньше нуля
4p² - 36 < 0, ⇒ p∈(-3, 3)