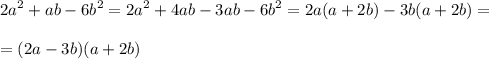
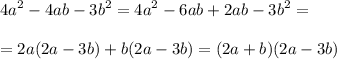
первого раствора взяли 20 литров, а второго - 80 литров.
Объяснение:
Пусть 30%- го раствора взяли х л, а 55%- го раствора - у л, тогда по условию
х + у = 100.
Кислоты в первом растворе 0,3•х л, во втором растворе 0,55•у л, всего 0,3х + 0,55у. По условию в получившейся смеси 0,5•100 = 50 (л) кислоты, составим уравнение: 0,3х + 0,55у = 50.
Оба условия выполняются одновременно, составим и решим систему уравнений:
{х + у = 100,
{0,3х + 0,55у = 50;
{ у = 100 - х,
{0,3х + 0,55у = 50;
{ у = 100 - х,
{0,3х + 0,55•(100 - х) = 50;
{ у = 100 - х,
{0,3х + 55 - 0,55х = 50;
{ у = 100 - х,
{- 0,25х = 50 - 55;
{ у = 100 - х,
{- 0,25х = - 5;
{ у = 100 - х,
{ х = 500:25;
{ у = 100 - х,
{ х = 20;
{ у = 100 - 20,
{ х = 20;
{ у = 80,
{ х = 20.
ответ: первого раствора взяли 20 литров, а второго - 80 литров.
ответ: 3) 9 км/час; 12 км/час.
Объяснение:
Пусть х км/ч - скорость первого велосипедиста, тогда (х + 3) км/ч - скорость второго велосипедиста.
Если первый велосипедист проехал до места встречи расстояние равное 45 км, то второй велосипедист проехал (93 - 45) км или 48 км.
Время в пути первого велосипедиста составило:
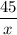 .
.
Время в пути второго велосипедиста составило:
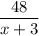 .
.
Зная, что первый велосипедист был в пути на 1 час дольше, чем второй велосипедист, составим и решим уравнение:
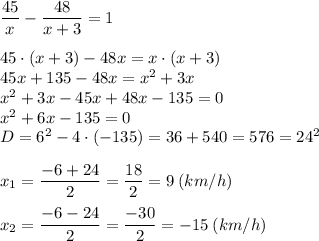
Второй корень не подходит, т.к. скорость не может иметь отрицательное значение.
Значит, скорость первого велосипедиста равна 9 км/ч.
Скорость второго велосипедиста равна:
9 + 3 = 125 (км/ч)