1
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
Tanusha13
10.02.2011
Алгебра
5 - 9 классы
ответ дан • проверенный экспертом
Дан квадрат со стороной 4 см. Середины его сторон являются вершинами второго квадрата. Середины сторон второго квадрата являются вершинами третьего квадрата и т. д. Доказать, что последовательность площадей этих квадратов является геометрической прогрессией. Найти площадь седьмого квадрата.
1
СМОТРЕТЬ ОТВЕТ
Войди чтобы добавить комментарий
ответ, проверенный экспертом
См. рисунок
BL=BK=0,5BC=2см
По теореме Пифагора найдем сторону вписанного квадрата KL
KL²=2BL² ⇒ KL=BL*√2=2√2 см.
Найдем во сколько раз сторона большого заданного квадрата, больше стороны вписанного
Соответственно площадь вписанного квадрата будет в 2 раза меньше площади большого заданного квадрата .
Если вписать в квадрат KLMN через середины его сторон квадрат, то площадь этого вписанного квадрата будет так же в 2 раза меньше чем площадь квадрата KLMN. И так далее Получается геометрическая прогрессия со знаменателем 0,5.
Площадь заданного большого квадрата S=a²=4²=16 см²
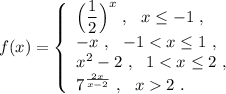
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х= -1, х=1 , х=2 .
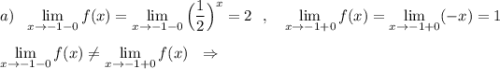
При х= -1 функция имеет разрыв 1 рода .

При х=1 функция непрерывна.
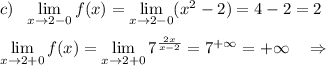
При х=5 функция имеет разрыв 2 рода .
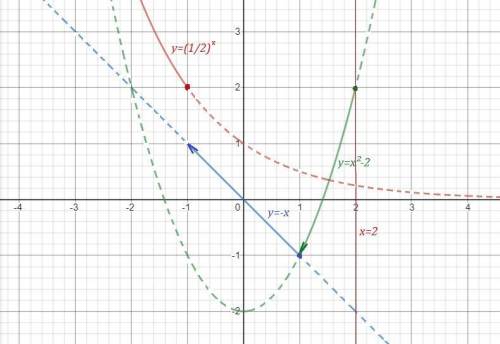
График функции нарисован сплошными линиями.
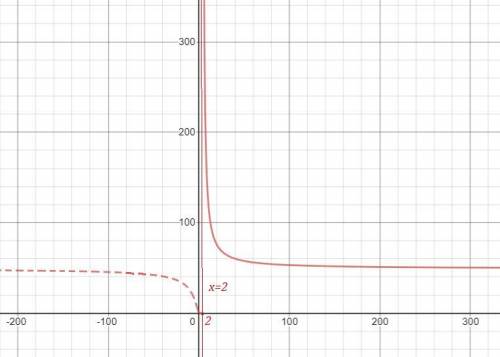
На 1 рисунке нет чертежа функции при х>2 , для которого прямая х=2 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>2 сплошной линией..