
1)
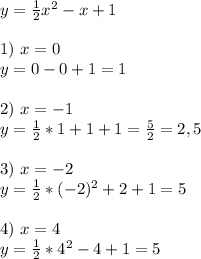
2)
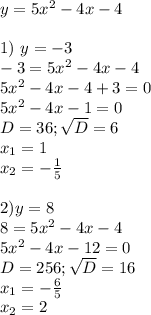
3)
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
5)
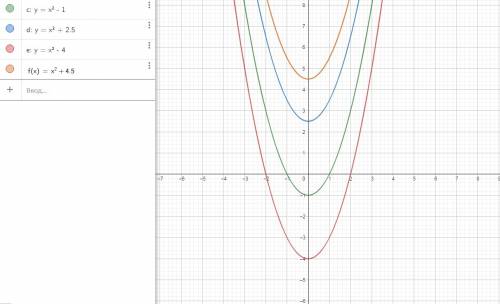
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)
55 (км/час) - скорость первого автомобиля
75 (км/час) - скорость второго автомобиля
Объяснение:
х - скорость первого автомобиля
х+20 - скорость второго автомобиля
206,25/х - время первого автомобиля
206,25/(х+20) - время второго автомобиля
По условию задачи разница во времени 1 час, уравнение:
206,25/х - 206,25/(х+20) = 1
Избавляемся от дробного выражения, общий знаменатель х(х+20), надписываем над числителями дополнительные множители:
206,25(х+20) - 206,25*х=1*х(х+20)
206,25х+4125-206,25х=х²+20х
-х²-20х+4125=0
х²+20х-4125=0, квадратное уравнение, ищем корни:
х₁,₂=(-20±√400+16500)/2
х₁,₂=(-20±√16900)/2
х₁,₂=(-20±130)/2
х₁= -75 отбрасываем, как отрицательный
х₂=110/2=55 (км/час) - скорость первого автомобиля
55+20=75 (км/час) - скорость второго автомобиля
Проверка:
206,25 : 55 = 3,75 (часа) время первого автомобиля
206,25 : 75 = 2,75 (часа) время второго автомобиля
Разница 1 час, всё верно.
ОДЗ
Перед третьей дробью меняем знак на минус и в знаменатели меняем местами,
будет х-5
Из первой дроби вычтем третью дробь.
Из того, что получилось вычитаем вторую дробь.
Дополнительный множитель к первой дроби х(3+х), а ко второй дроби 6(х-5)
Если должно получится -3(х+5)/х то числитель должен делиться хотя бы на 6, а он на 6 не делится.
А ты верно переписала?