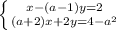
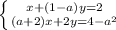
Система эквивалентных уравнений имеет бесконечное количество решений, это означает, что отношения коэффициентов при неизвестных и свободных членов должны быть равны.
отношения коэффициентов при 
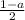отношения коэффициентов при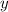 
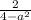отношения свободных членов
Получаем равенство.
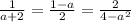
Решаем попарно.
1) Равенство первой и второй дробей
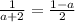
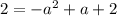
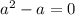
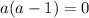
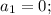
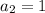
2) Равенство первой и третьей дробей
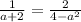
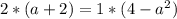
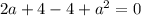
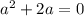
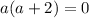
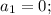
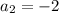
3) Равенство второй и третьей.
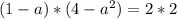
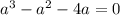
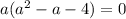
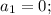
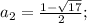
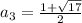
Общее решение: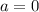 
ответ: при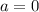
Такого значения параметра
b не существует.
Объяснение:
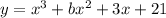
Находим производную
у'=
Приравниваем производную 0:
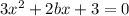
функция только убывает, если
на всей области определения
у'<0.
==>
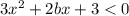
Рассмотрим уравнение:
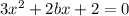
Это уравнение квадратичной
функции. Старший коэффици
ент а=3>0 ==>
если представить ее график
- это парабола, ветви которой
напрвлены вверх (парабола не
может полностью находиться
под осью абсцисс, так
как ее ветви бесконечно про
должаются вверх).
Вывод:
Условие у'<0 невыполнимо.
==> не существует такого зна
чения параметра b, когда функ
ция
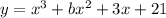
убывает на всей области оп
ределения.
а4b²-b4a²=a²b²(a-b)(a+b)