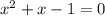
По теореме Виета
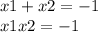
Нам надо вот такое:
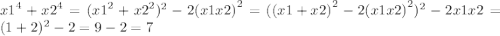
ответ: 7
Объяснение:
1)Найди решение неравенства. Начерти его на оси координат.
x>4.
На числовой оси отметить ноль по центру, от нуля вправо отложить четыре клеточки, это будет точка х=4. Теперь от этой точки штриховать вправо, как бы до + бесконечности. Неравенство строгое, поэтому точка 4 должна обозначаться маленьким кружком, пустым внутри.
ответ: x∈(4;+∞]
2)Отобрази решение неравенства 1≤z на оси координат. Запиши ответ в виде интервала.
На числовой оси отметить ноль по центру, от нуля вправо отложить одну клеточку, это будет точка z=1, от этой точки влево штриховать, как бы до - бесконечности.
Интервал: z ∈(-∞, 1)
⦁ Длины сторон треугольника обозначены как a, b и c. Какие из неравенств неверны?
Неясное задание.
3) Известно, что b>c.
Выбери верные неравенства:
7,9−b>7,9−c
−7,9b<−7,9c
7,9b>7,9c
b+7,9>c+7,9
b−7,9>c−7,9
Выделены верные неравенства.
ответ:8 см
ответ:8 смПошаговое объяснение:
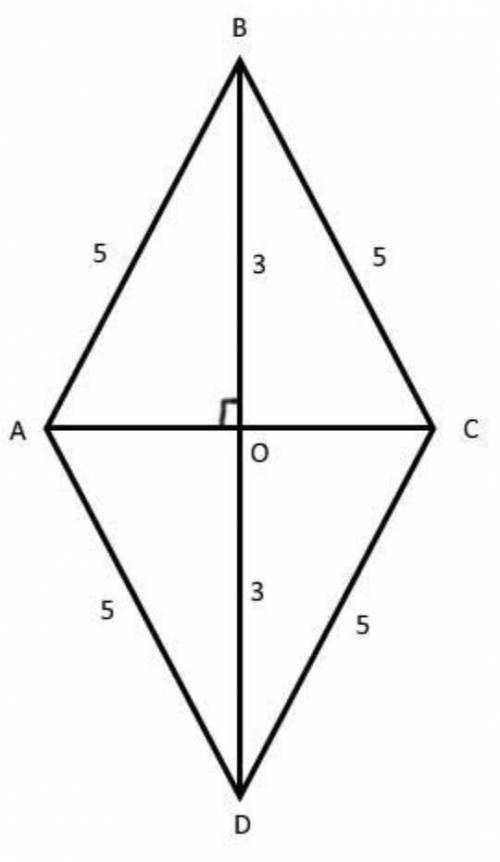
ответ:8 смПошаговое объяснение:Диагонали ромба пересекаются под прямым углом, а точка пересечения делит каждую пополам.
ответ:8 смПошаговое объяснение:Диагонали ромба пересекаются под прямым углом, а точка пересечения делит каждую пополам.Пусть диагональ ВD = 6 см, тогда BO = 3 см. По условию AB = 5 см.
ответ:8 смПошаговое объяснение:Диагонали ромба пересекаются под прямым углом, а точка пересечения делит каждую пополам.Пусть диагональ ВD = 6 см, тогда BO = 3 см. По условию AB = 5 см.По теореме Пифагора находим AO:
ответ:8 смПошаговое объяснение:Диагонали ромба пересекаются под прямым углом, а точка пересечения делит каждую пополам.Пусть диагональ ВD = 6 см, тогда BO = 3 см. По условию AB = 5 см.По теореме Пифагора находим AO:AC = 2*AO = 8 см
если дадите коронку я буду благодарна
Обратим сразу внимание на то, что уравнение имеет два корня. Для этого или посчитаем дискриминант, или заметим, что график функции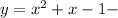 парабола, ветви которой направлены вверх, причем y(0)=-1<0, что гарантирует два пересечения этой параболы с осью OX (координаты точек пересечения и являются корнями уравнения).
парабола, ветви которой направлены вверх, причем y(0)=-1<0, что гарантирует два пересечения этой параболы с осью OX (координаты точек пересечения и являются корнями уравнения).
1-й По теореме Виета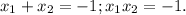
Далее,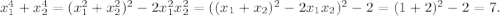
2-й Если x - корень уравнения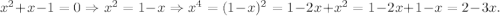
Таким образом,
ответ: 7