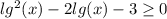
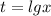
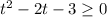
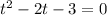
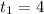
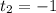
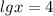
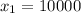
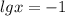
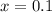
пусть О центр окружности, тогда
пусть ОК- перпендикуляр к ВС,
ОК и есть радиус треугольника
треугольники ОВС и КВО подобные, так как они оба прямоугольные, а угол В у них общий, тогда
ОК/ВО=ОС/ВС
ОС=6/2=3, ток как центр полувписаного круга делит пополам(равнобедренный ведь треугольник)
ВО^2=BC^2-OC^2=25-9=16
тогда
ОК=ОВ*ОС/ВС=4*3/5=12/5
тоесть радиус = 12/15
а далее расмотрим треугольник ВОК
BK^2=BO^2-OK^2=16-144/25=(400-144)/25=256/25=((16/5)^2
BK=16/5
КС=5-16/5=(25-16)/5=9/5
ответ
радиус 12/5
делит на отрезки
возле основы 9/5
возле вершины 16/5
Тогда
t² - 2t - 3 ≥ 0
t² - 2t - 3 = 0
D = b2 - 4ac = (-2)2 - 4·1·(-3) = 4 + 12 = 16
t1 = -1
t2 = 3
lgx = 3; x = 1000;
lgx = -1; x = 1/10;
x <= 1/10 и x >= 1000
ответ: x ∈ (-бесконечность, 1/10] U[1000, + бесконечность)