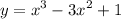
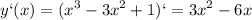
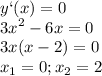
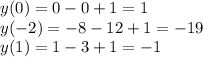
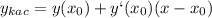
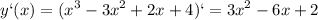
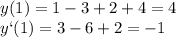
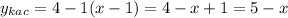
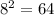 подходит
подходит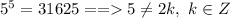 не подходит, так как непарная степень
не подходит, так как непарная степень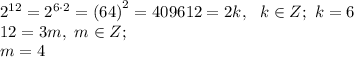
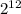 это будет квадрат 64
это будет квадрат 64 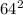 , и будет кубом от 16
, и будет кубом от 16 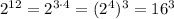 то-есть есть квадратом и кубон натуральніх чисел, поєтому не подходит
то-есть есть квадратом и кубон натуральніх чисел, поєтому не подходит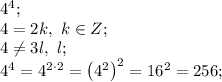 является квадратом натурального числа 16, и нету такого натурального числа, чтобы поднести в куб и получили данное
является квадратом натурального числа 16, и нету такого натурального числа, чтобы поднести в куб и получили данное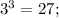 данное число уже является кубон натурального числа 3, а нутурального числа, чтобі в квадрате вышло 27 не существует
данное число уже является кубон натурального числа 3, а нутурального числа, чтобі в квадрате вышло 27 не существует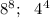
Перенося данное выражение в левую часть получаешь
2sin^2(2x)-sinx-1=0
Пусть sin2x=t
2t^2-t-1=0
T1=1; t2=-1/2
1)sin2x=1 => x=pi/4+pi*n, n э Z
2)sin2x=-1/2 => x=-pi/12+pi*k, k э Z
3)x=-5pi/12+pi*m, m э Z
3)
Пусть 3x=t
1-cos2t=tg t
Cos^2t+sin^2t-cos^2t+sin^2t=tg t
2sin^2t=tg t
2sin^2tcost=sint
Sint(2sintcost-1)=0
Sint(2sin2t-1)=0
1)sint=0
2)sin2t=1/2
T=pi*n
T=pi/12+pi*k
T=5pi/12+pi*m
X=pi*n/3
X=pi/36+pi*k/3
X=5pi/36+pi*m/3